Exploring Mode Connectivity for Pre-trained Language Models
Paper and Code
Oct 25, 2022
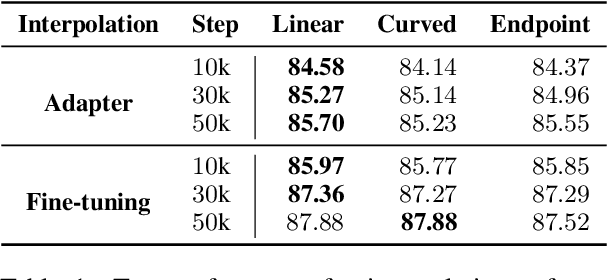

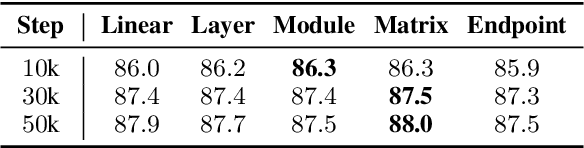
Recent years have witnessed the prevalent application of pre-trained language models (PLMs) in NLP. From the perspective of parameter space, PLMs provide generic initialization, starting from which high-performance minima could be found. Although plenty of works have studied how to effectively and efficiently adapt PLMs to high-performance minima, little is known about the connection of various minima reached under different adaptation configurations. In this paper, we investigate the geometric connections of different minima through the lens of mode connectivity, which measures whether two minima can be connected with a low-loss path. We conduct empirical analyses to investigate three questions: (1) how could hyperparameters, specific tuning methods, and training data affect PLM's mode connectivity? (2) How does mode connectivity change during pre-training? (3) How does the PLM's task knowledge change along the path connecting two minima? In general, exploring the mode connectivity of PLMs conduces to understanding the geometric connection of different minima, which may help us fathom the inner workings of PLM downstream adaptation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge