Exploiting Neighbor Effect: Conv-Agnostic GNNs Framework for Graphs with Heterophily

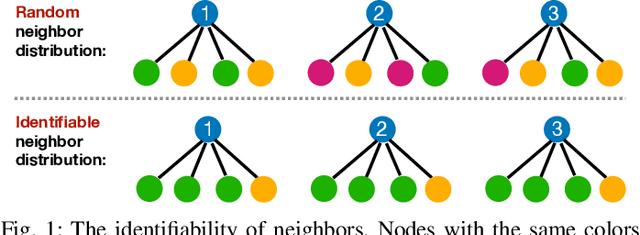
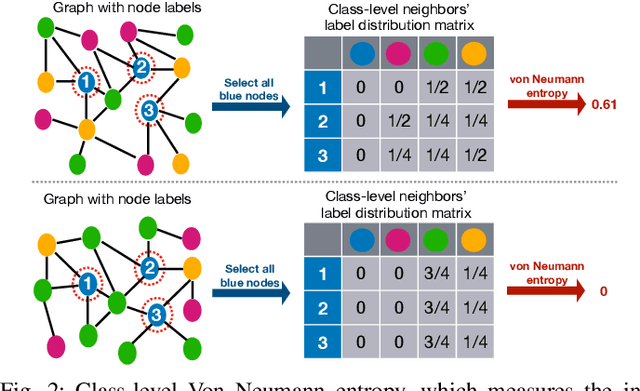
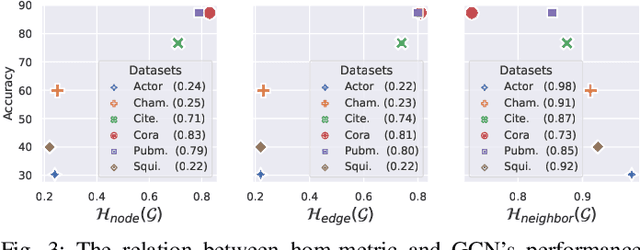
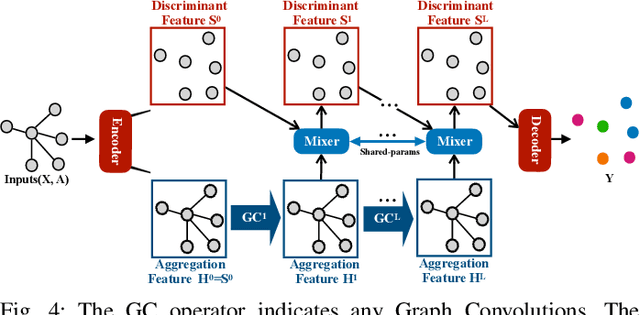
Due to the homophily assumption in graph convolution networks, a common consensus is that graph neural networks (GNNs) perform well on homophilic graphs but may fail on heterophilic graphs with many inter-class edges. In this work, we re-examine the heterophily problem of GNNs and investigate the feature aggregation of inter-class neighbors. Instead of treating the inter-class edges as harmful, under some conditions, we argue that they may provide helpful information for node classification from an entire neighbor's perspective. To better evaluate whether the neighbor is helpful for the downstream tasks, we present the concept of the neighbor effect of each node and use the von Neumann entropy to measure the randomness/identifiability of the neighbor distribution for each class. Moreover, we propose a Conv-Agnostic GNNs framework (CAGNNs) to enhance the performance of GNNs on heterophily datasets by learning the neighbor effect for each node. Specifically, we first decouple the feature of each node into the discriminative feature for downstream tasks and the aggregation feature for graph convolution. Then, we propose a shared mixer module for all layers to adaptively evaluate the neighbor effect of each node to incorporate the neighbor information. Experiments are performed on nine well-known benchmark datasets for the node classification task. The results indicate that our framework is able to improve the average prediction performance by 9.81%, 25.81%, and 20.61% for GIN, GAT, and GCN, respectively. Extensive ablation studies and robustness analysis further verify the effectiveness, robustness, and interpretability of our framework.