Enhancing Hyperbolic Graph Embeddings via Contrastive Learning
Paper and Code
Jan 21, 2022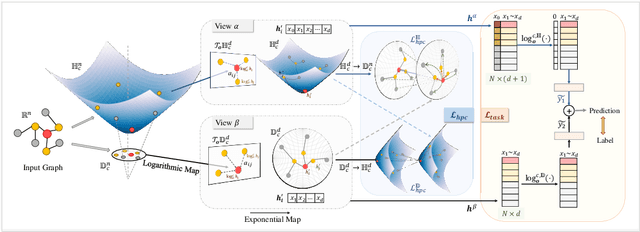
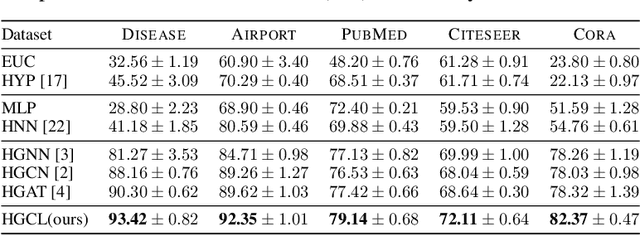
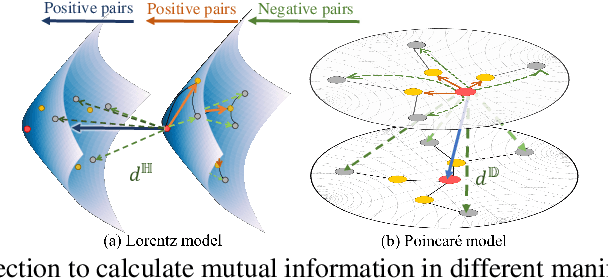

Recently, hyperbolic space has risen as a promising alternative for semi-supervised graph representation learning. Many efforts have been made to design hyperbolic versions of neural network operations. However, the inspiring geometric properties of this unique geometry have not been fully explored yet. The potency of graph models powered by the hyperbolic space is still largely underestimated. Besides, the rich information carried by abundant unlabelled samples is also not well utilized. Inspired by the recently active and emerging self-supervised learning, in this study, we attempt to enhance the representation power of hyperbolic graph models by drawing upon the advantages of contrastive learning. More specifically, we put forward a novel Hyperbolic Graph Contrastive Learning (HGCL) framework which learns node representations through multiple hyperbolic spaces to implicitly capture the hierarchical structure shared between different views. Then, we design a hyperbolic position consistency (HPC) constraint based on hyperbolic distance and the homophily assumption to make contrastive learning fit into hyperbolic space. Experimental results on multiple real-world datasets demonstrate the superiority of the proposed HGCL as it consistently outperforms competing methods by considerable margins for the node classification task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge