Emergence of Separable Manifolds in Deep Language Representations
Paper and Code
Jun 06, 2020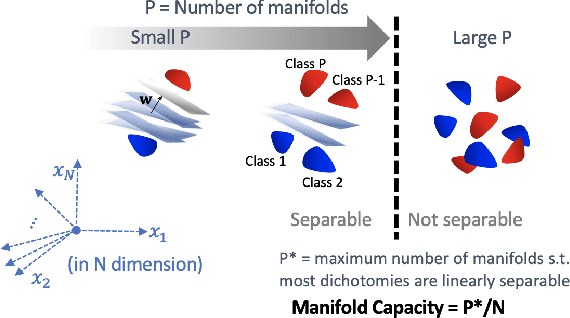
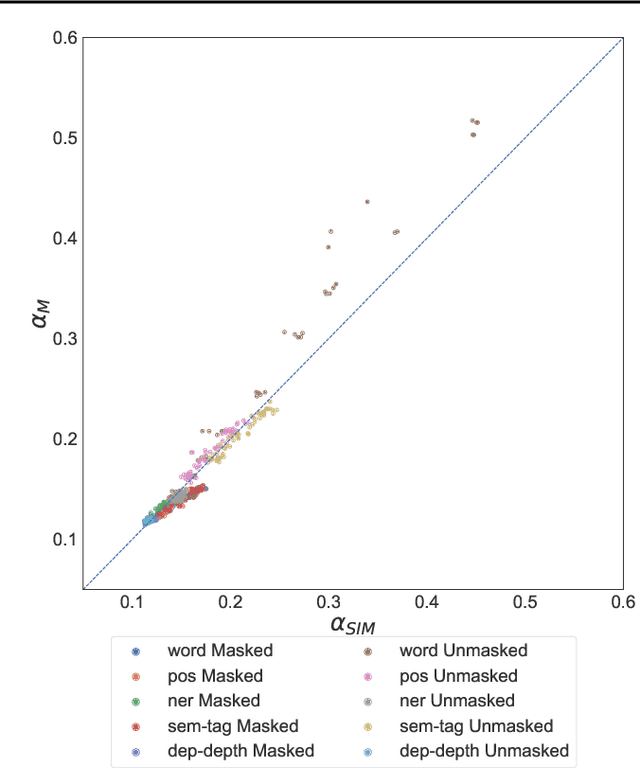
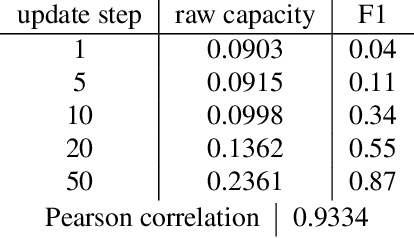
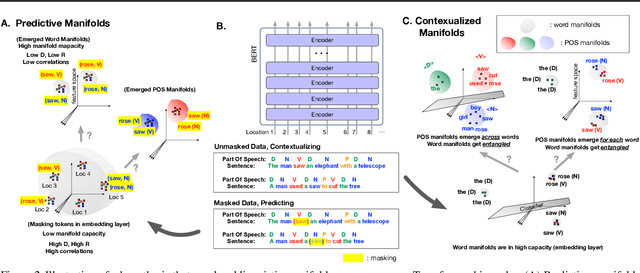
Artificial neural networks (ANNs) have shown much empirical success in solving perceptual tasks across various cognitive modalities. While they are only loosely inspired by the biological brain, recent studies report considerable similarities between representation extracted from task-optimized ANNs and neural populations in the brain. ANNs have subsequently become a popular model class to infer computational principles underlying complex cognitive functions, and in turn they have also emerged as a natural testbed for applying methods originally developed to probe information in neural populations. In this work, we utilize mean-field theoretic manifold analysis, a recent technique from computational neuroscience, to analyze the high dimensional geometry of language representations from large-scale contextual embedding models. We explore representations from different model families (BERT, RoBERTa, GPT-2, etc. ) and find evidence for emergence of linguistic manifold across layer depth (e.g., manifolds for part-of-speech and combinatory categorical grammar tags). We further observe that different encoding schemes used to obtain the representations lead to differences in whether these linguistic manifolds emerge in earlier or later layers of the network. In addition, we find that the emergence of linear separability in these manifolds is driven by a combined reduction of manifolds radius, dimensionality and inter-manifold correlations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge