Efficient Task-Specific Data Valuation for Nearest Neighbor Algorithms
Paper and Code
Sep 11, 2019

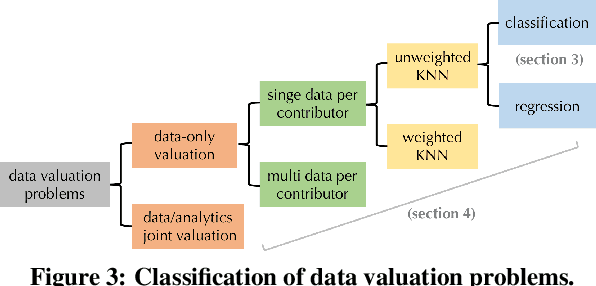

Given a data set $\mathcal{D}$ containing millions of data points and a data consumer who is willing to pay for \$$X$ to train a machine learning (ML) model over $\mathcal{D}$, how should we distribute this \$$X$ to each data point to reflect its "value"? In this paper, we define the "relative value of data" via the Shapley value, as it uniquely possesses properties with appealing real-world interpretations, such as fairness, rationality and decentralizability. For general, bounded utility functions, the Shapley value is known to be challenging to compute: to get Shapley values for all $N$ data points, it requires $O(2^N)$ model evaluations for exact computation and $O(N\log N)$ for $(\epsilon, \delta)$-approximation. In this paper, we focus on one popular family of ML models relying on $K$-nearest neighbors ($K$NN). The most surprising result is that for unweighted $K$NN classifiers and regressors, the Shapley value of all $N$ data points can be computed, exactly, in $O(N\log N)$ time -- an exponential improvement on computational complexity! Moreover, for $(\epsilon, \delta)$-approximation, we are able to develop an algorithm based on Locality Sensitive Hashing (LSH) with only sublinear complexity $O(N^{h(\epsilon,K)}\log N)$ when $\epsilon$ is not too small and $K$ is not too large. We empirically evaluate our algorithms on up to $10$ million data points and even our exact algorithm is up to three orders of magnitude faster than the baseline approximation algorithm. The LSH-based approximation algorithm can accelerate the value calculation process even further. We then extend our algorithms to other scenarios such as (1) weighed $K$NN classifiers, (2) different data points are clustered by different data curators, and (3) there are data analysts providing computation who also requires proper valuation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge