Efficient Kernel UCB for Contextual Bandits

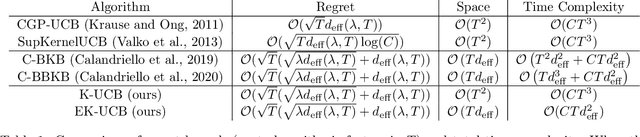
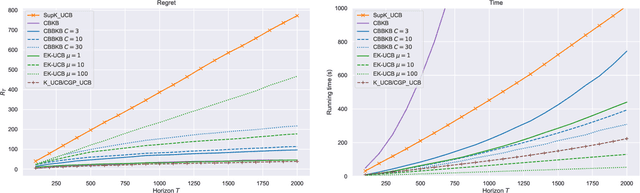
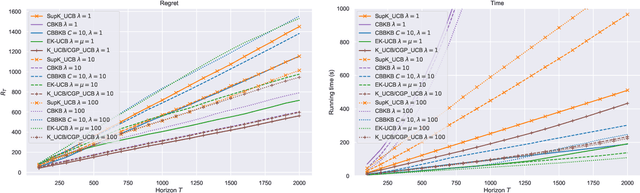
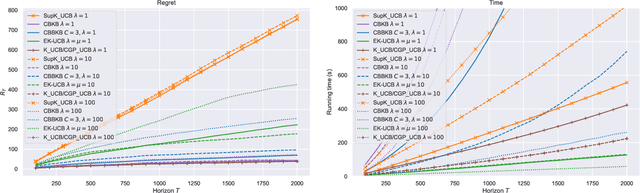
In this paper, we tackle the computational efficiency of kernelized UCB algorithms in contextual bandits. While standard methods require a O(CT^3) complexity where T is the horizon and the constant C is related to optimizing the UCB rule, we propose an efficient contextual algorithm for large-scale problems. Specifically, our method relies on incremental Nystrom approximations of the joint kernel embedding of contexts and actions. This allows us to achieve a complexity of O(CTm^2) where m is the number of Nystrom points. To recover the same regret as the standard kernelized UCB algorithm, m needs to be of order of the effective dimension of the problem, which is at most O(\sqrt(T)) and nearly constant in some cases.