Effects of Exponential Gaussian Distribution on (Double Sampling) Randomized Smoothing
Paper and Code
Jun 04, 2024

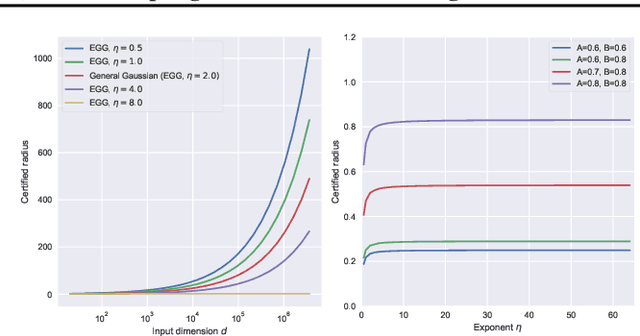

Randomized Smoothing (RS) is currently a scalable certified defense method providing robustness certification against adversarial examples. Although significant progress has been achieved in providing defenses against $\ell_p$ adversaries, the interaction between the smoothing distribution and the robustness certification still remains vague. In this work, we comprehensively study the effect of two families of distributions, named Exponential Standard Gaussian (ESG) and Exponential General Gaussian (EGG) distributions, on Randomized Smoothing and Double Sampling Randomized Smoothing (DSRS). We derive an analytic formula for ESG's certified radius, which converges to the origin formula of RS as the dimension $d$ increases. Additionally, we prove that EGG can provide tighter constant factors than DSRS in providing $\Omega(\sqrt{d})$ lower bounds of $\ell_2$ certified radius, and thus further addresses the curse of dimensionality in RS. Our experiments on real-world datasets confirm our theoretical analysis of the ESG distributions, that they provide almost the same certification under different exponents $\eta$ for both RS and DSRS. In addition, EGG
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge