Effective Generation of Feasible Solutions for Integer Programming via Guided Diffusion
Paper and Code
Jun 18, 2024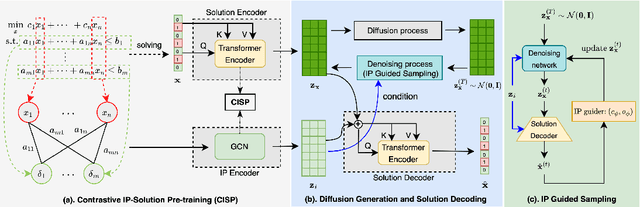
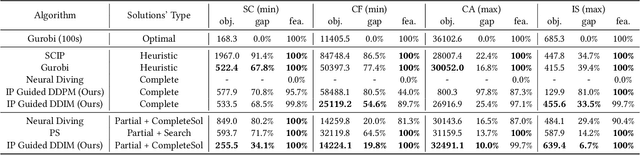
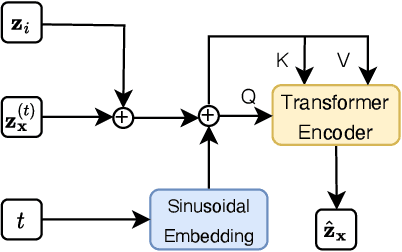

Feasible solutions are crucial for Integer Programming (IP) since they can substantially speed up the solving process. In many applications, similar IP instances often exhibit similar structures and shared solution distributions, which can be potentially modeled by deep learning methods. Unfortunately, existing deep-learning-based algorithms, such as Neural Diving and Predict-and-search framework, are limited to generating only partial feasible solutions, and they must rely on solvers like SCIP and Gurobi to complete the solutions for a given IP problem. In this paper, we propose a novel framework that generates complete feasible solutions end-to-end. Our framework leverages contrastive learning to characterize the relationship between IP instances and solutions, and learns latent embeddings for both IP instances and their solutions. Further, the framework employs diffusion models to learn the distribution of solution embeddings conditioned on IP representations, with a dedicated guided sampling strategy that accounts for both constraints and objectives. We empirically evaluate our framework on four typical datasets of IP problems, and show that it effectively generates complete feasible solutions with a high probability (> 89.7 \%) without the reliance of Solvers and the quality of solutions is comparable to the best heuristic solutions from Gurobi. Furthermore, by integrating our method's sampled partial solutions with the CompleteSol heuristic from SCIP, the resulting feasible solutions outperform those from state-of-the-art methods across all datasets, exhibiting a 3.7 to 33.7\% improvement in the gap to optimal values, and maintaining a feasible ratio of over 99.7\% for all datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge