Doubly Robust Data-Driven Distributionally Robust Optimization
Paper and Code
May 19, 2017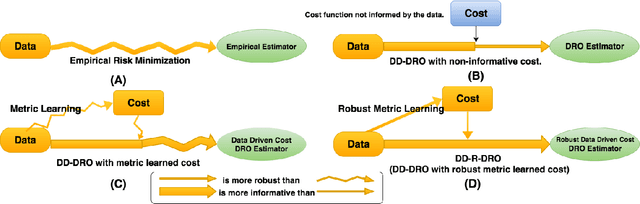
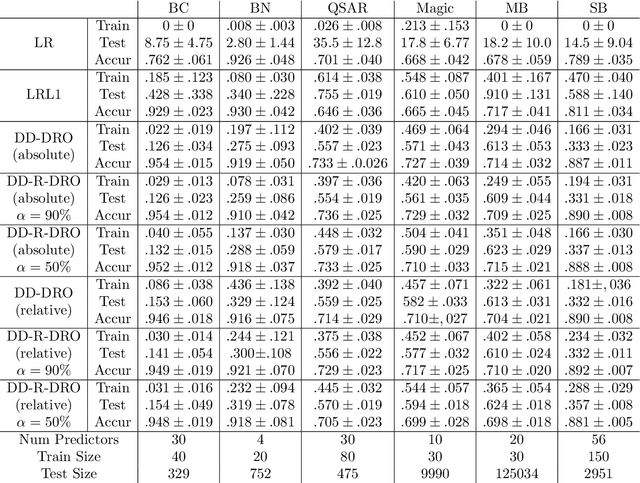
Data-driven Distributionally Robust Optimization (DD-DRO) via optimal transport has been shown to encompass a wide range of popular machine learning algorithms. The distributional uncertainty size is often shown to correspond to the regularization parameter. The type of regularization (e.g. the norm used to regularize) corresponds to the shape of the distributional uncertainty. We propose a data-driven robust optimization methodology to inform the transportation cost underlying the definition of the distributional uncertainty. We show empirically that this additional layer of robustification, which produces a method we called doubly robust data-driven distributionally robust optimization (DD-R-DRO), allows to enhance the generalization properties of regularized estimators while reducing testing error relative to state-of-the-art classifiers in a wide range of data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge