Double Bubble, Toil and Trouble: Enhancing Certified Robustness through Transitivity
Paper and Code
Oct 12, 2022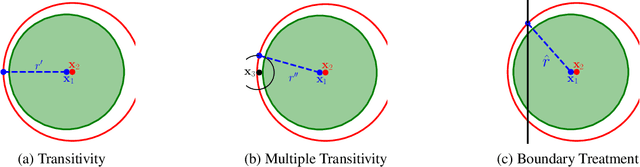
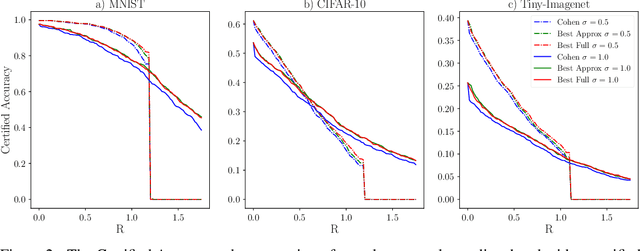
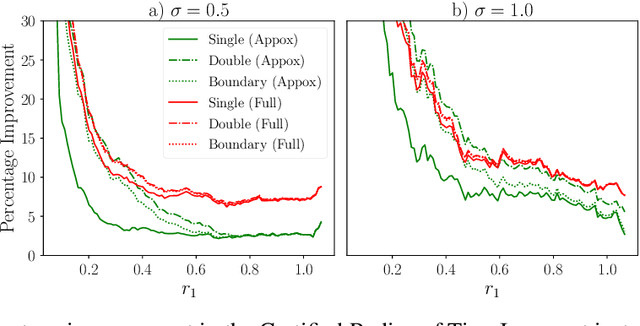
In response to subtle adversarial examples flipping classifications of neural network models, recent research has promoted certified robustness as a solution. There, invariance of predictions to all norm-bounded attacks is achieved through randomised smoothing of network inputs. Today's state-of-the-art certifications make optimal use of the class output scores at the input instance under test: no better radius of certification (under the $L_2$ norm) is possible given only these score. However, it is an open question as to whether such lower bounds can be improved using local information around the instance under test. In this work, we demonstrate how today's "optimal" certificates can be improved by exploiting both the transitivity of certifications, and the geometry of the input space, giving rise to what we term Geometrically-Informed Certified Robustness. By considering the smallest distance to points on the boundary of a set of certifications this approach improves certifications for more than $80\%$ of Tiny-Imagenet instances, yielding an on average $5 \%$ increase in the associated certification. When incorporating training time processes that enhance the certified radius, our technique shows even more promising results, with a uniform $4$ percentage point increase in the achieved certified radius.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge