DLME: Deep Local-flatness Manifold Embedding
Paper and Code
Jul 07, 2022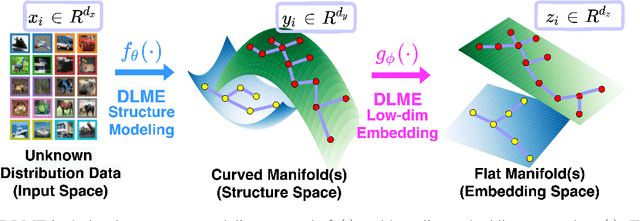
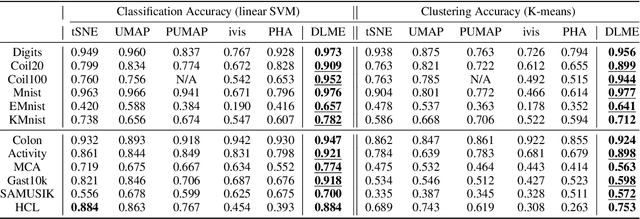
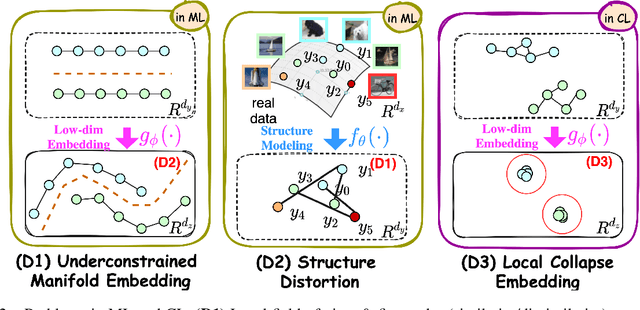
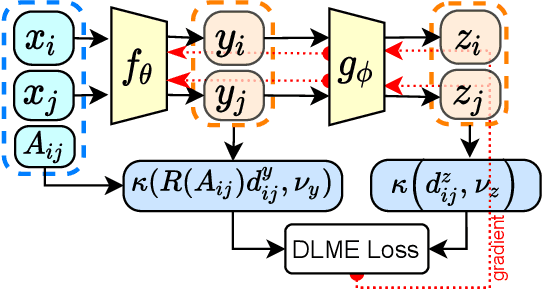
Manifold learning~(ML) aims to find low-dimensional embedding from high-dimensional data. Previous works focus on handcraft or easy datasets with simple and ideal scenarios; however, we find they perform poorly on real-world datasets with under-sampling data. Generally, ML methods primarily model data structure and subsequently process a low-dimensional embedding, where the poor local connectivity of under-sampling data in the former step and inappropriate optimization objectives in the later step will lead to \emph{structural distortion} and \emph{underconstrained embedding}. To solve this problem, we propose Deep Local-flatness Manifold Embedding (DLME), a novel ML framework to obtain reliable manifold embedding by reducing distortion. Our proposed DLME constructs semantic manifolds by data augmentation and overcomes \emph{structural distortion} problems with the help of its smooth framework. To overcome \emph{underconstrained embedding}, we design a specific loss for DLME and mathematically demonstrate that it leads to a more suitable embedding based on our proposed Local Flatness Assumption. In the experiments, by showing the effectiveness of DLME on downstream classification, clustering, and visualization tasks with three types of datasets (toy, biological, and image), our experimental results show that DLME outperforms SOTA ML \& contrastive learning (CL) methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge