Distributed stochastic proximal algorithm with random reshuffling for non-smooth finite-sum optimization

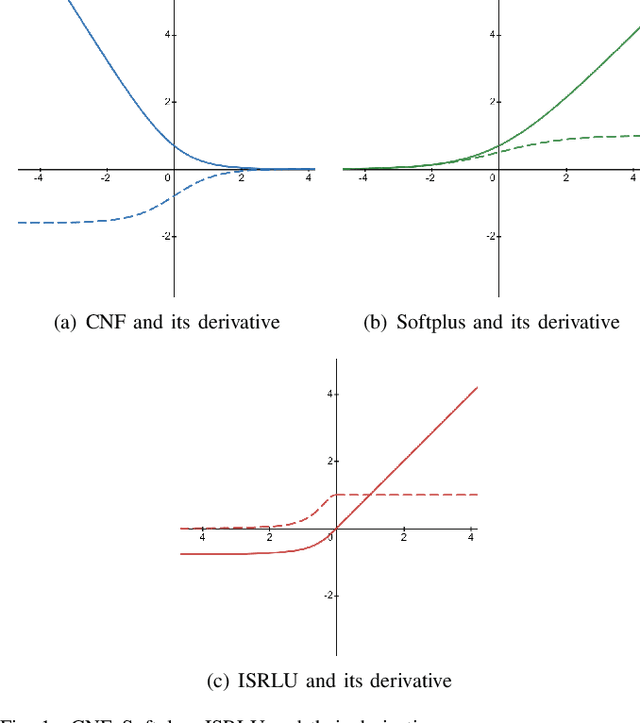
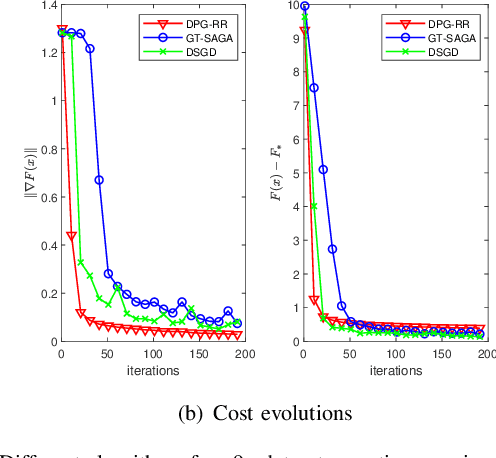
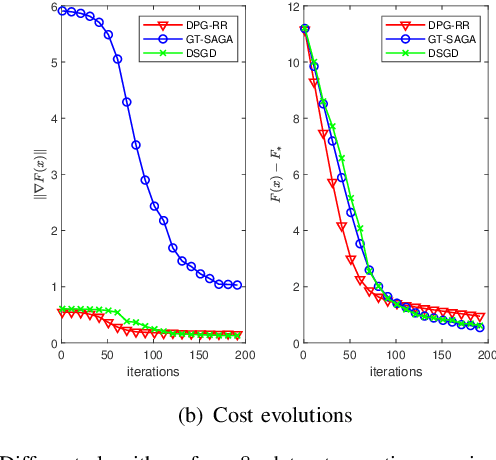
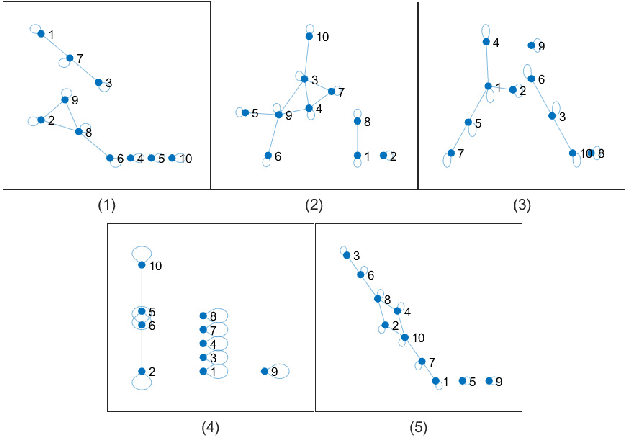
The non-smooth finite-sum minimization is a fundamental problem in machine learning. This paper develops a distributed stochastic proximal-gradient algorithm with random reshuffling to solve the finite-sum minimization over time-varying multi-agent networks. The objective function is a sum of differentiable convex functions and non-smooth regularization. Each agent in the network updates local variables with a constant step-size by local information and cooperates to seek an optimal solution. We prove that local variable estimates generated by the proposed algorithm achieve consensus and are attracted to a neighborhood of the optimal solution in expectation with an $\mathcal{O}(\frac{1}{T}+\frac{1}{\sqrt{T}})$ convergence rate. In addition, this paper shows that the steady-state error of the objective function can be arbitrarily small by choosing small enough step-sizes. Finally, some comparative simulations are provided to verify the convergence performance of the proposed algorithm.