Distributed Non-Convex Optimization with Sublinear Speedup under Intermittent Client Availability
Paper and Code
Feb 18, 2020
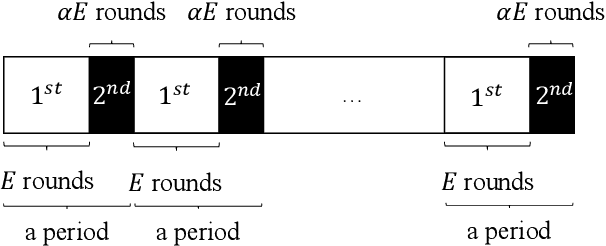
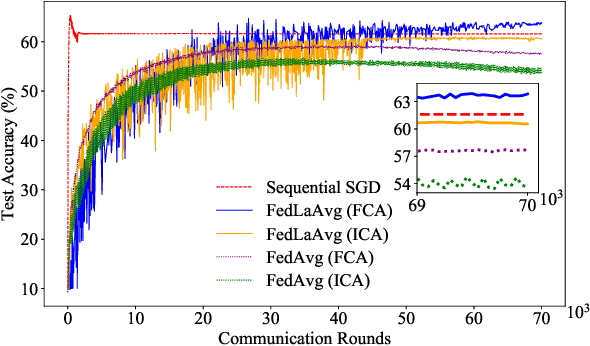

Federated learning is a new distributed machine learning framework, where a bunch of heterogeneous clients collaboratively train a model without sharing training data. In this work, we consider a practical and ubiquitous issue in federated learning: intermittent client availability, where the set of eligible clients may change during the training process. Such an intermittent client availability model would significantly deteriorate the performance of the classical Federated Averaging algorithm (FedAvg for short). We propose a simple distributed non-convex optimization algorithm, called Federated Latest Averaging (FedLaAvg for short), which leverages the latest gradients of all clients, even when the clients are not available, to jointly update the global model in each iteration. Our theoretical analysis shows that FedLaAvg attains the convergence rate of $O(1/(N^{1/4} T^{1/2}))$, achieving a sublinear speedup with respect to the total number of clients. We implement and evaluate FedLaAvg with the CIFAR-10 dataset. The evaluation results demonstrate that FedLaAvg indeed reaches a sublinear speedup and achieves 4.23% higher test accuracy than FedAvg.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge