Distance Metric Learning using Graph Convolutional Networks: Application to Functional Brain Networks
Paper and Code
Jun 14, 2017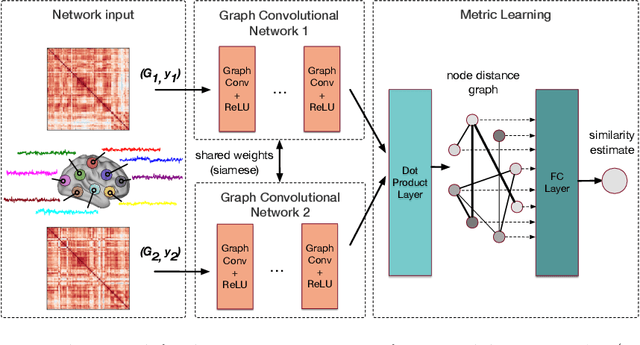

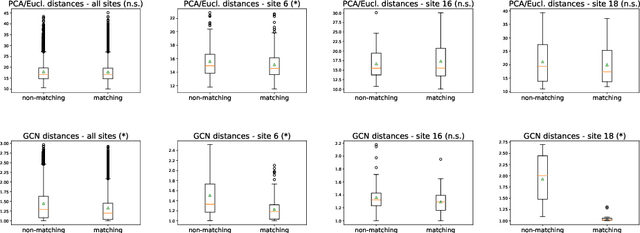
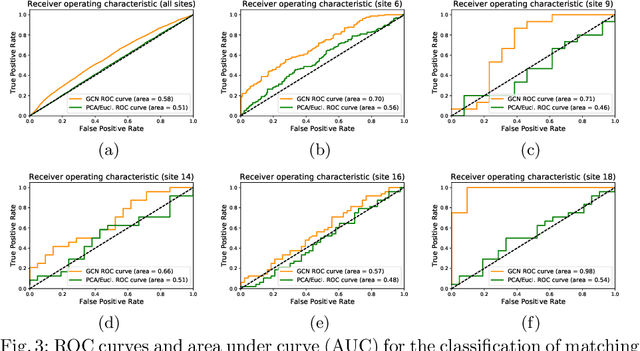
Evaluating similarity between graphs is of major importance in several computer vision and pattern recognition problems, where graph representations are often used to model objects or interactions between elements. The choice of a distance or similarity metric is, however, not trivial and can be highly dependent on the application at hand. In this work, we propose a novel metric learning method to evaluate distance between graphs that leverages the power of convolutional neural networks, while exploiting concepts from spectral graph theory to allow these operations on irregular graphs. We demonstrate the potential of our method in the field of connectomics, where neuronal pathways or functional connections between brain regions are commonly modelled as graphs. In this problem, the definition of an appropriate graph similarity function is critical to unveil patterns of disruptions associated with certain brain disorders. Experimental results on the ABIDE dataset show that our method can learn a graph similarity metric tailored for a clinical application, improving the performance of a simple k-nn classifier by 11.9% compared to a traditional distance metric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge