Disentangling Observed Causal Effects from Latent Confounders using Method of Moments
Paper and Code
Jan 17, 2021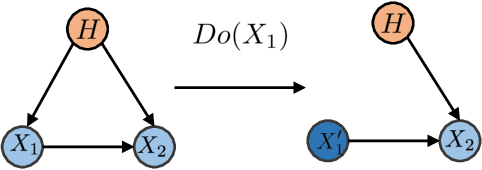
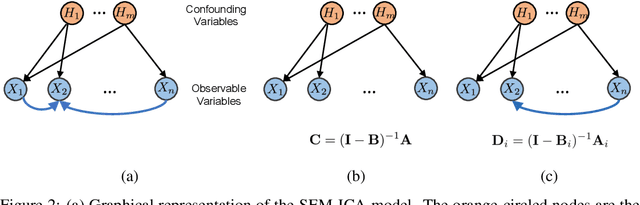
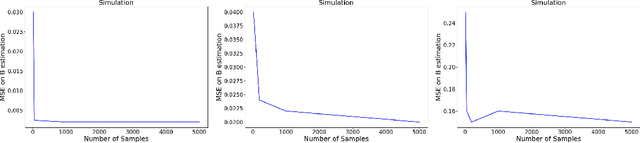
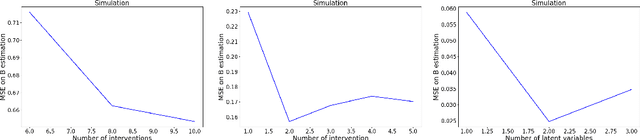
Discovering the complete set of causal relations among a group of variables is a challenging unsupervised learning problem. Often, this challenge is compounded by the fact that there are latent or hidden confounders. When only observational data is available, the problem is ill-posed, i.e. the causal relationships are non-identifiable unless strong modeling assumptions are made. When interventions are available, we provide guarantees on identifiability and learnability under mild assumptions. We assume a linear structural equation model (SEM) with independent latent factors and directed acyclic graph (DAG) relationships among the observables. Since the latent variable inference is based on independent component analysis (ICA), we call this model SEM-ICA. We use the method of moments principle to establish model identifiability. We develop efficient algorithms based on coupled tensor decomposition with linear constraints to obtain scalable and guaranteed solutions. Thus, we provide a principled approach to tackling the joint problem of causal discovery and latent variable inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge