Discrete Optimal Graph Clustering
Paper and Code
Apr 25, 2019
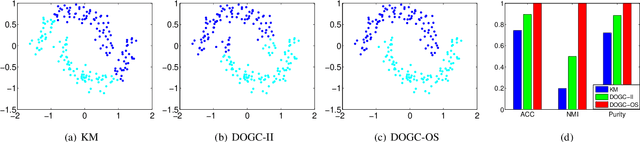


Graph based clustering is one of the major clustering methods. Most of it work in three separate steps: similarity graph construction, clustering label relaxing and label discretization with k-means. Such common practice has three disadvantages: 1) the predefined similarity graph is often fixed and may not be optimal for the subsequent clustering. 2) the relaxing process of cluster labels may cause significant information loss. 3) label discretization may deviate from the real clustering result since k-means is sensitive to the initialization of cluster centroids. To tackle these problems, in this paper, we propose an effective discrete optimal graph clustering (DOGC) framework. A structured similarity graph that is theoretically optimal for clustering performance is adaptively learned with a guidance of reasonable rank constraint. Besides, to avoid the information loss, we explicitly enforce a discrete transformation on the intermediate continuous label, which derives a tractable optimization problem with discrete solution. Further, to compensate the unreliability of the learned labels and enhance the clustering accuracy, we design an adaptive robust module that learns prediction function for the unseen data based on the learned discrete cluster labels. Finally, an iterative optimization strategy guaranteed with convergence is developed to directly solve the clustering results. Extensive experiments conducted on both real and synthetic datasets demonstrate the superiority of our proposed methods compared with several state-of-the-art clustering approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge