Deep Probabilistic Graph Matching
Paper and Code
Jan 05, 2022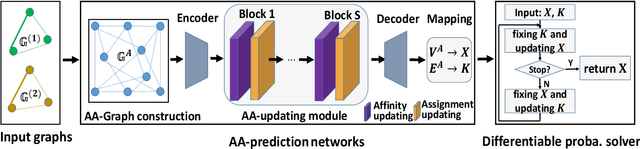
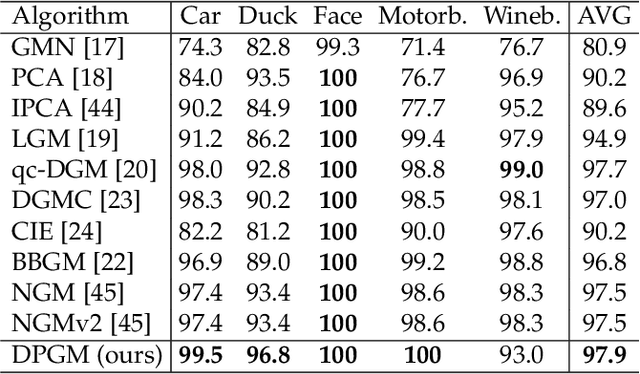
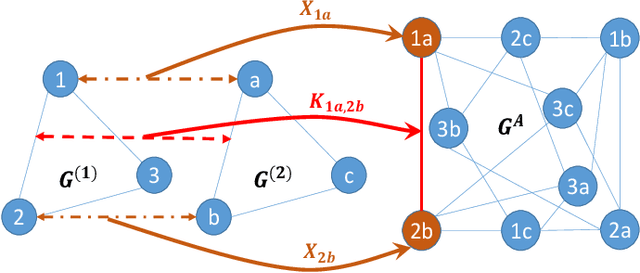
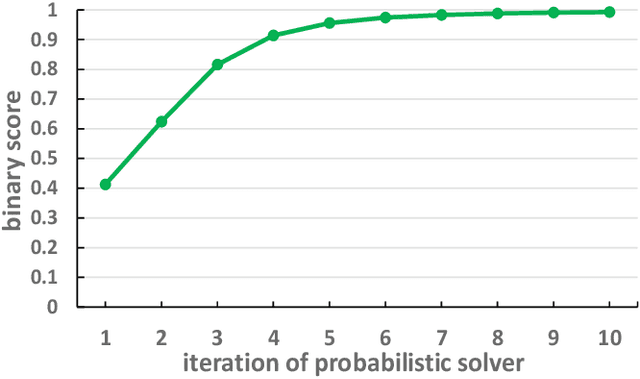
Most previous learning-based graph matching algorithms solve the \textit{quadratic assignment problem} (QAP) by dropping one or more of the matching constraints and adopting a relaxed assignment solver to obtain sub-optimal correspondences. Such relaxation may actually weaken the original graph matching problem, and in turn hurt the matching performance. In this paper we propose a deep learning-based graph matching framework that works for the original QAP without compromising on the matching constraints. In particular, we design an affinity-assignment prediction network to jointly learn the pairwise affinity and estimate the node assignments, and we then develop a differentiable solver inspired by the probabilistic perspective of the pairwise affinities. Aiming to obtain better matching results, the probabilistic solver refines the estimated assignments in an iterative manner to impose both discrete and one-to-one matching constraints. The proposed method is evaluated on three popularly tested benchmarks (Pascal VOC, Willow Object and SPair-71k), and it outperforms all previous state-of-the-arts on all benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge