Deep Learning-Based Solvability of Underdetermined Inverse Problems in Medical Imaging
Paper and Code
Jan 07, 2020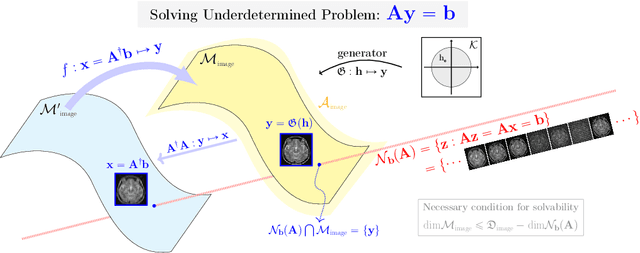
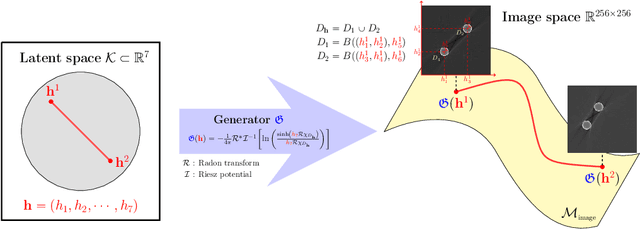
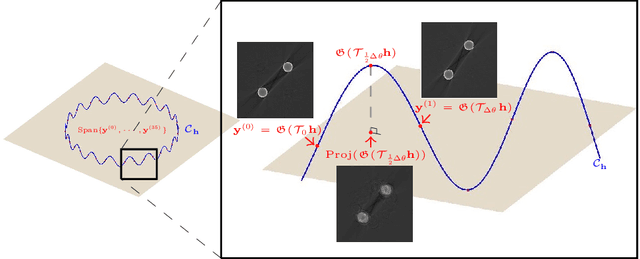
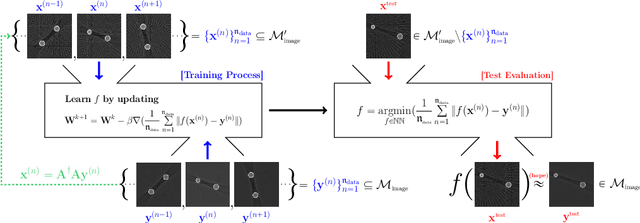
Recently, with the significant developments in deep learning techniques, solving underdetermined inverse problems has become one of the major concerns in the medical imaging domain. Typical examples include undersampled magnetic resonance imaging, interior tomography, and sparse-view computed tomography, where deep learning techniques have achieved excellent performances. Although deep learning methods appear to overcome the limitations of existing mathematical methods when handling various underdetermined problems, there is a lack of rigorous mathematical foundations that would allow us to elucidate the reasons for the remarkable performance of deep learning methods. This study focuses on learning the causal relationship regarding the structure of the training data suitable for deep learning, to solve highly underdetermined inverse problems. We observe that a majority of the problems of solving underdetermined linear systems in medical imaging are highly non-linear. Furthermore, we analyze if a desired reconstruction map can be learnable from the training data and underdetermined system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge