Deep Gamblers: Learning to Abstain with Portfolio Theory

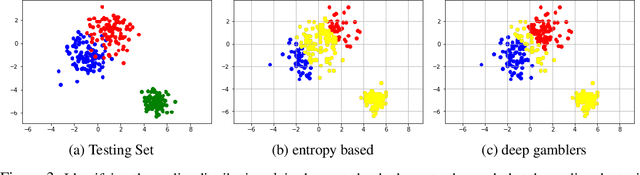
We deal with the \textit{selective classification} problem (supervised-learning problem with a rejection option), where we want to achieve the best performance at a certain level of coverage of the data. We transform the original $m$-class classification problem to $(m+1)$-class where the $(m+1)$-th class represents the model abstaining from making a prediction due to uncertainty. Inspired by portfolio theory, we propose a loss function for the selective classification problem based on the doubling rate of gambling. We show that minimizing this loss function has a natural interpretation as maximizing the return of a \textit{horse race}, where a player aims to balance between betting on an outcome (making a prediction) when confident and reserving one's winnings (abstaining) when not confident. This loss function allows us to train neural networks and characterize the uncertainty of prediction in an end-to-end fashion. In comparison with previous methods, our method requires almost no modification to the model inference algorithm or neural architecture. Experimentally, we show that our method can identify both uncertain and outlier data points, and achieves strong results on SVHN and CIFAR10 at various coverages of the data.