Deep Bayesian Quadrature Policy Optimization

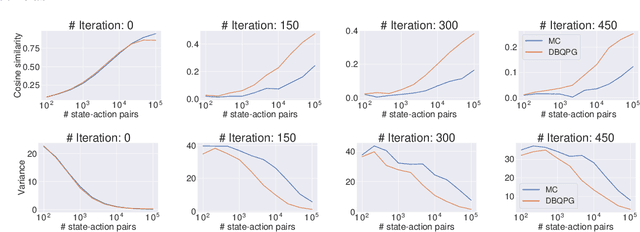
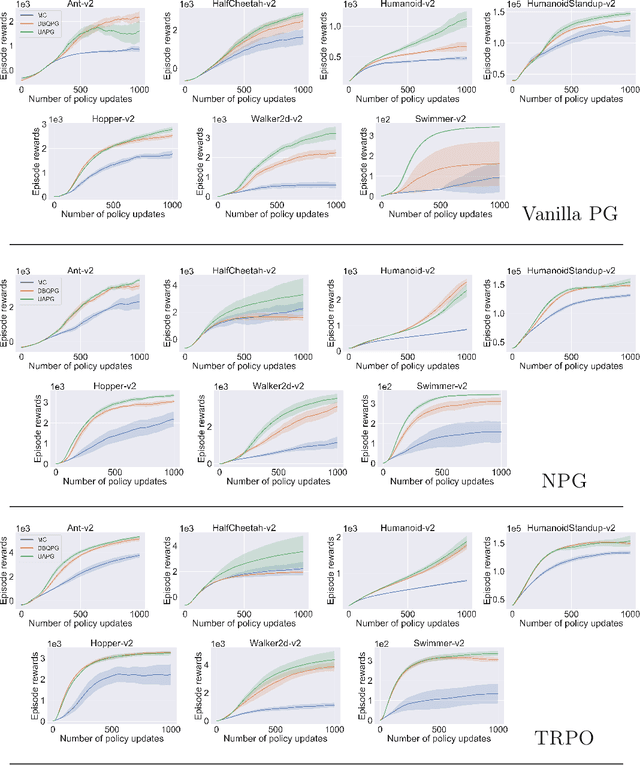
We study the problem of obtaining accurate policy gradient estimates. This challenge manifests in how best to estimate the policy gradient integral equation using a finite number of samples. Monte-Carlo methods have been the default choice for this purpose, despite suffering from high variance in the gradient estimates. On the other hand, more sample efficient alternatives like Bayesian quadrature methods are less scalable due to their high computational complexity. In this work, we propose deep Bayesian quadrature policy gradient (DBQPG), a computationally efficient high-dimensional generalization of Bayesian quadrature, to estimate the policy gradient integral equation. We show that DBQPG can substitute Monte-Carlo estimation in policy gradient methods, and demonstrate its effectiveness on a set of continuous control benchmarks for robotic locomotion. In comparison to Monte-Carlo estimation, DBQPG provides (i) more accurate gradient estimates with a significantly lower variance, (ii) a consistent improvement in the sample complexity and average return for several on-policy deep policy gradient algorithms, and, (iii) a methodological way to quantify the uncertainty in gradient estimation that can be incorporated to further improve the performance.