Decentralized Graph-Based Multi-Agent Reinforcement Learning Using Reward Machines
Paper and Code
Sep 30, 2021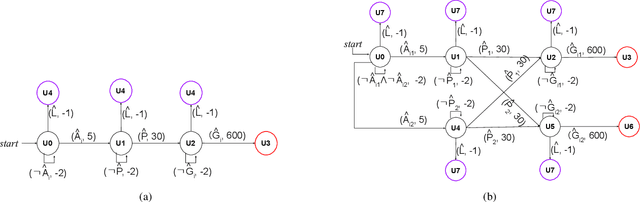
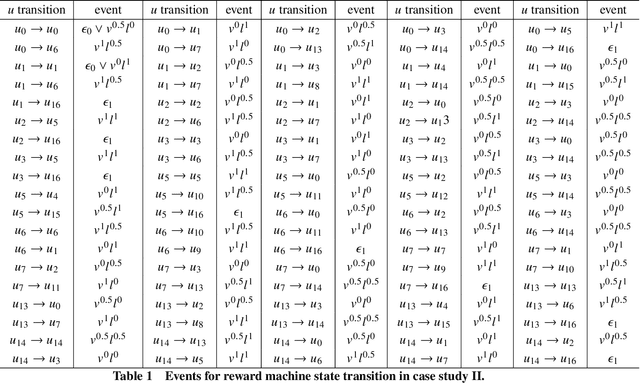

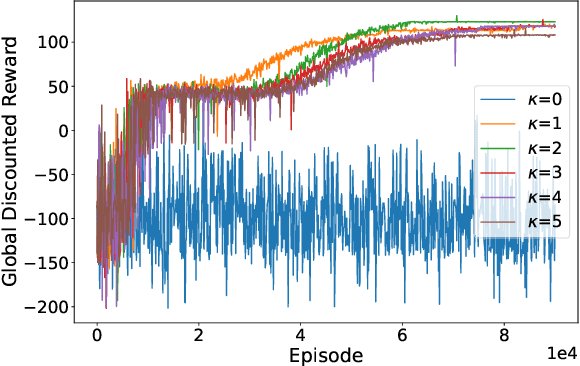
In multi-agent reinforcement learning (MARL), it is challenging for a collection of agents to learn complex temporally extended tasks. The difficulties lie in computational complexity and how to learn the high-level ideas behind reward functions. We study the graph-based Markov Decision Process (MDP) where the dynamics of neighboring agents are coupled. We use a reward machine (RM) to encode each agent's task and expose reward function internal structures. RM has the capacity to describe high-level knowledge and encode non-Markovian reward functions. We propose a decentralized learning algorithm to tackle computational complexity, called decentralized graph-based reinforcement learning using reward machines (DGRM), that equips each agent with a localized policy, allowing agents to make decisions independently, based on the information available to the agents. DGRM uses the actor-critic structure, and we introduce the tabular Q-function for discrete state problems. We show that the dependency of Q-function on other agents decreases exponentially as the distance between them increases. Furthermore, the complexity of DGRM is related to the local information size of the largest $\kappa$-hop neighborhood, and DGRM can find an $O(\rho^{\kappa+1})$-approximation of a stationary point of the objective function. To further improve efficiency, we also propose the deep DGRM algorithm, using deep neural networks to approximate the Q-function and policy function to solve large-scale or continuous state problems. The effectiveness of the proposed DGRM algorithm is evaluated by two case studies, UAV package delivery and COVID-19 pandemic mitigation. Experimental results show that local information is sufficient for DGRM and agents can accomplish complex tasks with the help of RM. DGRM improves the global accumulated reward by 119% compared to the baseline in the case of COVID-19 pandemic mitigation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge