Dataless Quadratic Neural Networks for the Maximum Independent Set Problem
Paper and Code
Jun 27, 2024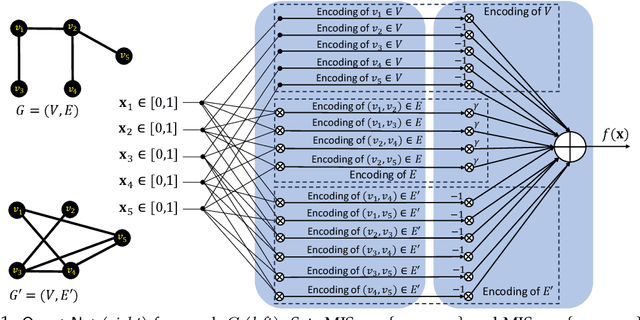



Combinatorial Optimization (CO) plays a crucial role in addressing various significant problems, among them the challenging Maximum Independent Set (MIS) problem. In light of recent advancements in deep learning methods, efforts have been directed towards leveraging data-driven learning approaches, typically rooted in supervised learning and reinforcement learning, to tackle the NP-hard MIS problem. However, these approaches rely on labeled datasets, exhibit weak generalization, and often depend on problem-specific heuristics. Recently, ReLU-based dataless neural networks were introduced to address combinatorial optimization problems. This paper introduces a novel dataless quadratic neural network formulation, featuring a continuous quadratic relaxation for the MIS problem. Notably, our method eliminates the need for training data by treating the given MIS instance as a trainable entity. More specifically, the graph structure and constraints of the MIS instance are used to define the structure and parameters of the neural network such that training it on a fixed input provides a solution to the problem, thereby setting it apart from traditional supervised or reinforcement learning approaches. By employing a gradient-based optimization algorithm like ADAM and leveraging an efficient off-the-shelf GPU parallel implementation, our straightforward yet effective approach demonstrates competitive or superior performance compared to state-of-the-art learning-based methods. Another significant advantage of our approach is that, unlike exact and heuristic solvers, the running time of our method scales only with the number of nodes in the graph, not the number of edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge