Data-driven detrending of nonstationary fractal time series with echo state networks
Paper and Code
Oct 03, 2016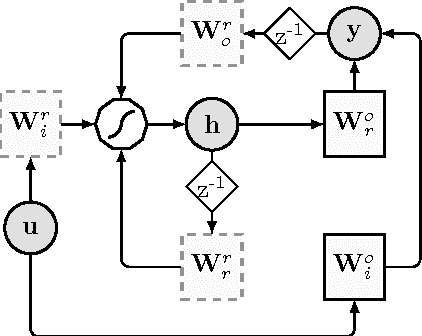

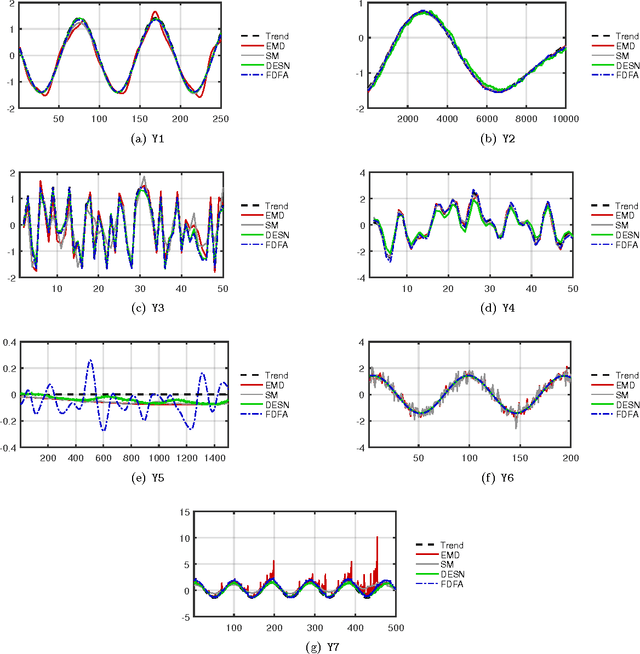
In this paper, we propose a novel data-driven approach for removing trends (detrending) from nonstationary, fractal and multifractal time series. We consider real-valued time series relative to measurements of an underlying dynamical system that evolves through time. We assume that such a dynamical process is predictable to a certain degree by means of a class of recurrent networks called Echo State Network (ESN), which are capable to model a generic dynamical process. In order to isolate the superimposed (multi)fractal component of interest, we define a data-driven filter by leveraging on the ESN prediction capability to identify the trend component of a given input time series. Specifically, the (estimated) trend is removed from the original time series and the residual signal is analyzed with the multifractal detrended fluctuation analysis procedure to verify the correctness of the detrending procedure. In order to demonstrate the effectiveness of the proposed technique, we consider several synthetic time series consisting of different types of trends and fractal noise components with known characteristics. We also process a real-world dataset, the sunspot time series, which is well-known for its multifractal features and has recently gained attention in the complex systems field. Results demonstrate the validity and generality of the proposed detrending method based on ESNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge