Data Distribution Valuation
Paper and Code
Oct 06, 2024
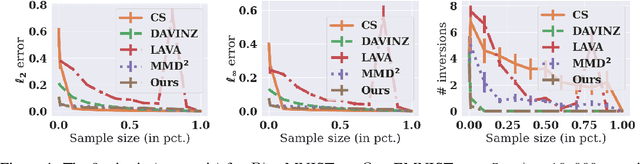

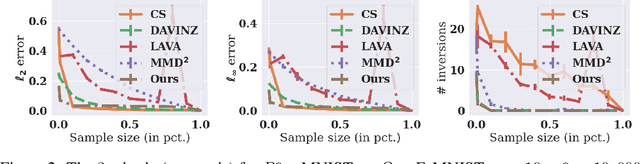
Data valuation is a class of techniques for quantitatively assessing the value of data for applications like pricing in data marketplaces. Existing data valuation methods define a value for a discrete dataset. However, in many use cases, users are interested in not only the value of the dataset, but that of the distribution from which the dataset was sampled. For example, consider a buyer trying to evaluate whether to purchase data from different vendors. The buyer may observe (and compare) only a small preview sample from each vendor, to decide which vendor's data distribution is most useful to the buyer and purchase. The core question is how should we compare the values of data distributions from their samples? Under a Huber characterization of the data heterogeneity across vendors, we propose a maximum mean discrepancy (MMD)-based valuation method which enables theoretically principled and actionable policies for comparing data distributions from samples. We empirically demonstrate that our method is sample-efficient and effective in identifying valuable data distributions against several existing baselines, on multiple real-world datasets (e.g., network intrusion detection, credit card fraud detection) and downstream applications (classification, regression).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge