Curvature Graph Neural Network
Paper and Code
Jun 30, 2021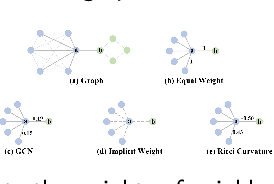

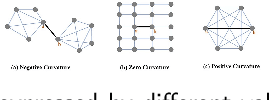
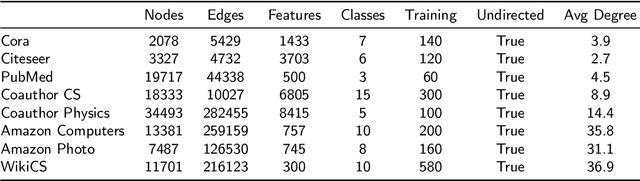
Graph neural networks (GNNs) have achieved great success in many graph-based tasks. Much work is dedicated to empowering GNNs with the adaptive locality ability, which enables measuring the importance of neighboring nodes to the target node by a node-specific mechanism. However, the current node-specific mechanisms are deficient in distinguishing the importance of nodes in the topology structure. We believe that the structural importance of neighboring nodes is closely related to their importance in aggregation. In this paper, we introduce discrete graph curvature (the Ricci curvature) to quantify the strength of structural connection of pairwise nodes. And we propose Curvature Graph Neural Network (CGNN), which effectively improves the adaptive locality ability of GNNs by leveraging the structural property of graph curvature. To improve the adaptability of curvature to various datasets, we explicitly transform curvature into the weights of neighboring nodes by the necessary Negative Curvature Processing Module and Curvature Normalization Module. Then, we conduct numerous experiments on various synthetic datasets and real-world datasets. The experimental results on synthetic datasets show that CGNN effectively exploits the topology structure information, and the performance is improved significantly. CGNN outperforms the baselines on 5 dense node classification benchmark datasets. This study deepens the understanding of how to utilize advanced topology information and assign the importance of neighboring nodes from the perspective of graph curvature and encourages us to bridge the gap between graph theory and neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge