Consistency Diffusion Bridge Models
Paper and Code
Oct 31, 2024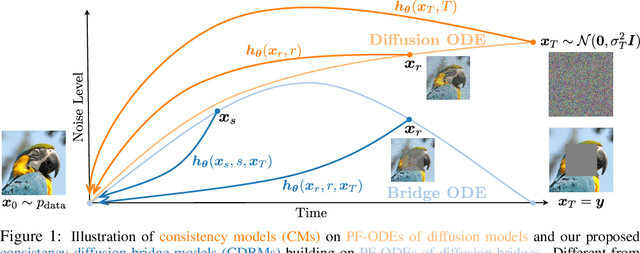

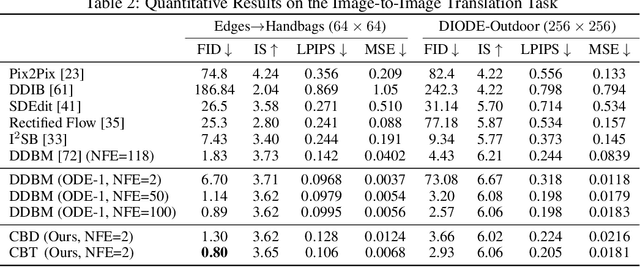
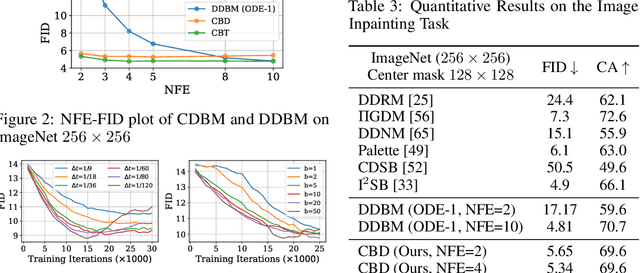
Diffusion models (DMs) have become the dominant paradigm of generative modeling in a variety of domains by learning stochastic processes from noise to data. Recently, diffusion denoising bridge models (DDBMs), a new formulation of generative modeling that builds stochastic processes between fixed data endpoints based on a reference diffusion process, have achieved empirical success across tasks with coupled data distribution, such as image-to-image translation. However, DDBM's sampling process typically requires hundreds of network evaluations to achieve decent performance, which may impede their practical deployment due to high computational demands. In this work, inspired by the recent advance of consistency models in DMs, we tackle this problem by learning the consistency function of the probability-flow ordinary differential equation (PF-ODE) of DDBMs, which directly predicts the solution at a starting step given any point on the ODE trajectory. Based on a dedicated general-form ODE solver, we propose two paradigms: consistency bridge distillation and consistency bridge training, which is flexible to apply on DDBMs with broad design choices. Experimental results show that our proposed method could sample $4\times$ to $50\times$ faster than the base DDBM and produce better visual quality given the same step in various tasks with pixel resolution ranging from $64 \times 64$ to $256 \times 256$, as well as supporting downstream tasks such as semantic interpolation in the data space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge