Comparative Evaluation of Action Recognition Methods via Riemannian Manifolds, Fisher Vectors and GMMs: Ideal and Challenging Conditions
Paper and Code
Oct 04, 2016
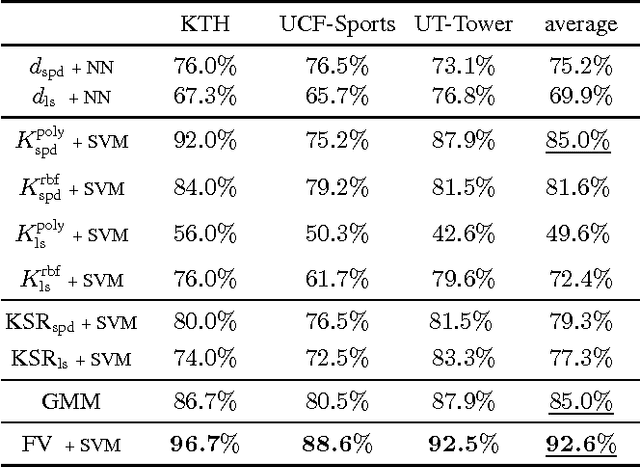

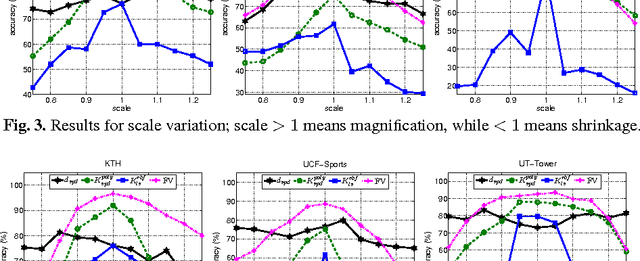
We present a comparative evaluation of various techniques for action recognition while keeping as many variables as possible controlled. We employ two categories of Riemannian manifolds: symmetric positive definite matrices and linear subspaces. For both categories we use their corresponding nearest neighbour classifiers, kernels, and recent kernelised sparse representations. We compare against traditional action recognition techniques based on Gaussian mixture models and Fisher vectors (FVs). We evaluate these action recognition techniques under ideal conditions, as well as their sensitivity in more challenging conditions (variations in scale and translation). Despite recent advancements for handling manifolds, manifold based techniques obtain the lowest performance and their kernel representations are more unstable in the presence of challenging conditions. The FV approach obtains the highest accuracy under ideal conditions. Moreover, FV best deals with moderate scale and translation changes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge