Communication-Efficient Robust Federated Learning Over Heterogeneous Datasets
Paper and Code
Jun 17, 2020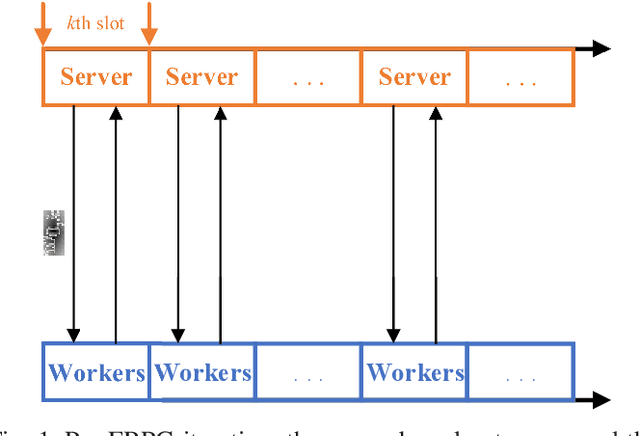
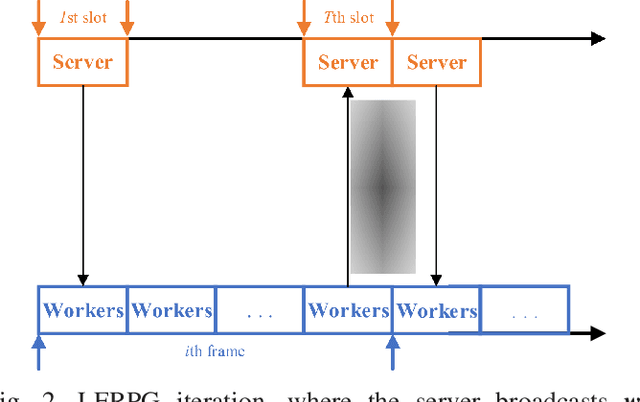
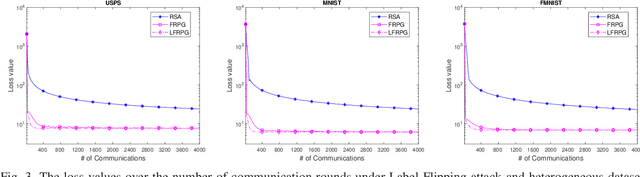
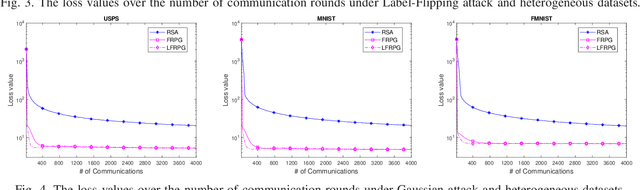
This work investigates fault-resilient federated learning when the data samples are non-uniformly distributed across workers, and the number of faulty workers is unknown to the central server. In the presence of adversarially faulty workers who may strategically corrupt datasets, the local messages exchanged (e.g., local gradients and/or local model parameters) can be unreliable, and thus the vanilla stochastic gradient descent (SGD) algorithm is not guaranteed to converge. Recently developed algorithms improve upon vanilla SGD by providing robustness to faulty workers at the price of slowing down convergence. To remedy this limitation, the present work introduces a fault-resilient proximal gradient (FRPG) algorithm that relies on Nesterov's acceleration technique. To reduce the communication overhead of FRPG, a local (L) FRPG algorithm is also developed to allow for intermittent server-workers parameter exchanges. For strongly convex loss functions, FRPG and LFRPG have provably faster convergence rates than a benchmark robust stochastic aggregation algorithm. Moreover, LFRPG converges faster than FRPG while using the same communication rounds. Numerical tests performed on various real datasets confirm the accelerated convergence of FRPG and LFRPG over the robust stochastic aggregation benchmark and competing alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge