Communication-Efficient Federated Learning through Importance Sampling
Paper and Code
Jun 25, 2023
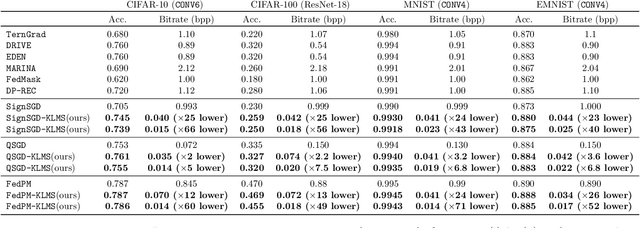
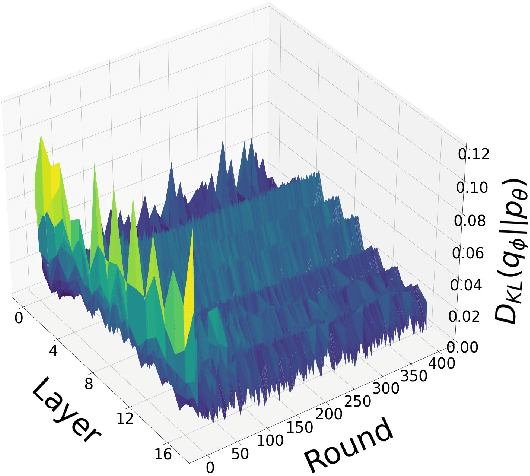
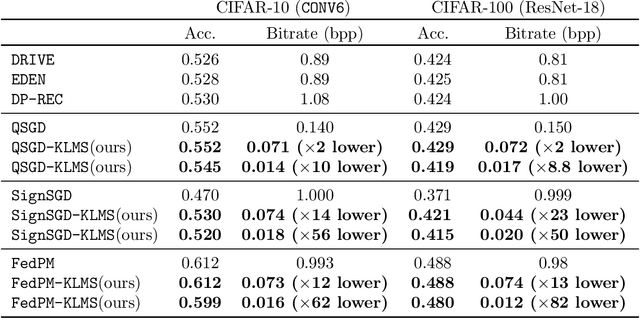
The high communication cost of sending model updates from the clients to the server is a significant bottleneck for scalable federated learning (FL). Among existing approaches, state-of-the-art bitrate-accuracy tradeoffs have been achieved using stochastic compression methods -- in which the client $n$ sends a sample from a client-only probability distribution $q_{\phi^{(n)}}$, and the server estimates the mean of the clients' distributions using these samples. However, such methods do not take full advantage of the FL setup where the server, throughout the training process, has side information in the form of a pre-data distribution $p_{\theta}$ that is close to the client's distribution $q_{\phi^{(n)}}$ in Kullback-Leibler (KL) divergence. In this work, we exploit this closeness between the clients' distributions $q_{\phi^{(n)}}$'s and the side information $p_{\theta}$ at the server, and propose a framework that requires approximately $D_{KL}(q_{\phi^{(n)}}|| p_{\theta})$ bits of communication. We show that our method can be integrated into many existing stochastic compression frameworks such as FedPM, Federated SGLD, and QSGD to attain the same (and often higher) test accuracy with up to $50$ times reduction in the bitrate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge