CARL-G: Clustering-Accelerated Representation Learning on Graphs
Paper and Code
Jun 12, 2023
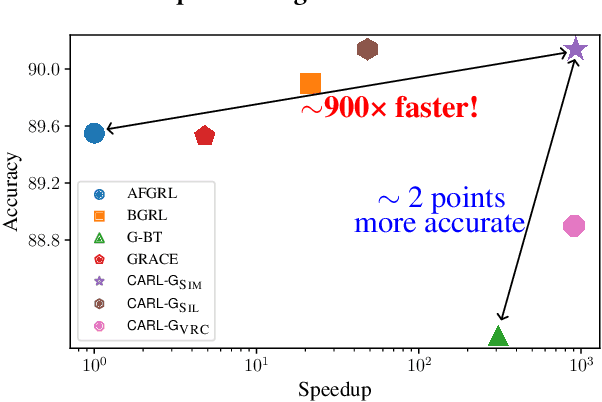
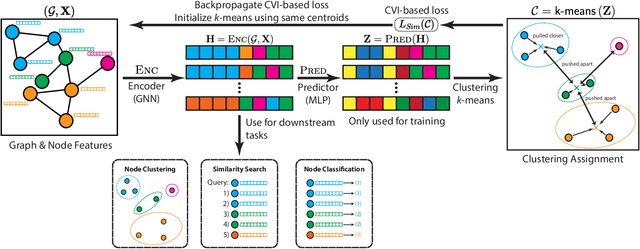
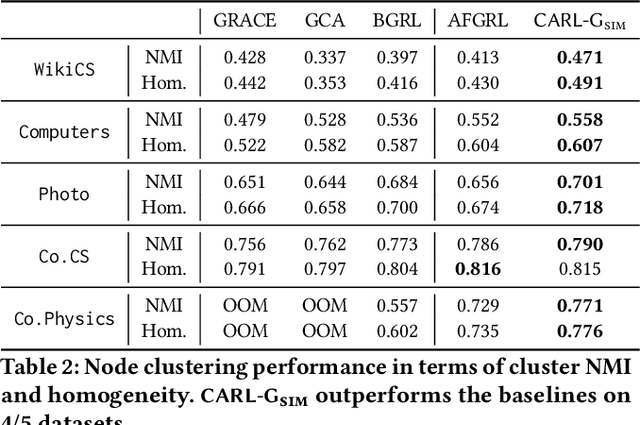
Self-supervised learning on graphs has made large strides in achieving great performance in various downstream tasks. However, many state-of-the-art methods suffer from a number of impediments, which prevent them from realizing their full potential. For instance, contrastive methods typically require negative sampling, which is often computationally costly. While non-contrastive methods avoid this expensive step, most existing methods either rely on overly complex architectures or dataset-specific augmentations. In this paper, we ask: Can we borrow from classical unsupervised machine learning literature in order to overcome those obstacles? Guided by our key insight that the goal of distance-based clustering closely resembles that of contrastive learning: both attempt to pull representations of similar items together and dissimilar items apart. As a result, we propose CARL-G - a novel clustering-based framework for graph representation learning that uses a loss inspired by Cluster Validation Indices (CVIs), i.e., internal measures of cluster quality (no ground truth required). CARL-G is adaptable to different clustering methods and CVIs, and we show that with the right choice of clustering method and CVI, CARL-G outperforms node classification baselines on 4/5 datasets with up to a 79x training speedup compared to the best-performing baseline. CARL-G also performs at par or better than baselines in node clustering and similarity search tasks, training up to 1,500x faster than the best-performing baseline. Finally, we also provide theoretical foundations for the use of CVI-inspired losses in graph representation learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge