Calibrating Segmentation Networks with Margin-based Label Smoothing

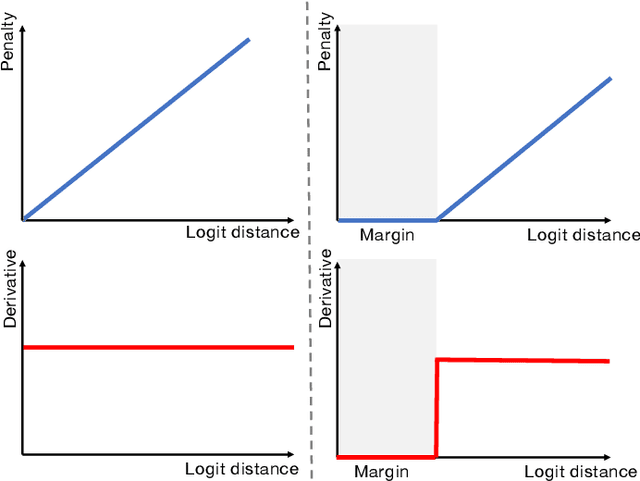
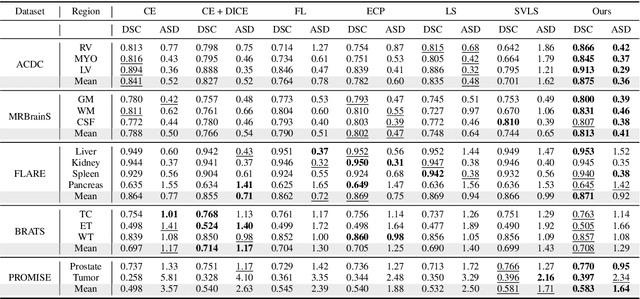
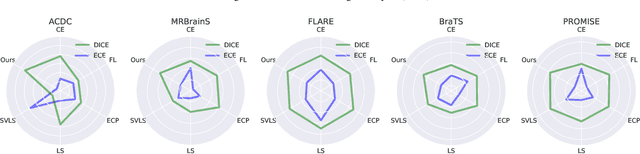
Despite the undeniable progress in visual recognition tasks fueled by deep neural networks, there exists recent evidence showing that these models are poorly calibrated, resulting in over-confident predictions. The standard practices of minimizing the cross entropy loss during training promote the predicted softmax probabilities to match the one-hot label assignments. Nevertheless, this yields a pre-softmax activation of the correct class that is significantly larger than the remaining activations, which exacerbates the miscalibration problem. Recent observations from the classification literature suggest that loss functions that embed implicit or explicit maximization of the entropy of predictions yield state-of-the-art calibration performances. Despite these findings, the impact of these losses in the relevant task of calibrating medical image segmentation networks remains unexplored. In this work, we provide a unifying constrained-optimization perspective of current state-of-the-art calibration losses. Specifically, these losses could be viewed as approximations of a linear penalty (or a Lagrangian term) imposing equality constraints on logit distances. This points to an important limitation of such underlying equality constraints, whose ensuing gradients constantly push towards a non-informative solution, which might prevent from reaching the best compromise between the discriminative performance and calibration of the model during gradient-based optimization. Following our observations, we propose a simple and flexible generalization based on inequality constraints, which imposes a controllable margin on logit distances. Comprehensive experiments on a variety of public medical image segmentation benchmarks demonstrate that our method sets novel state-of-the-art results on these tasks in terms of network calibration, whereas the discriminative performance is also improved.