C-GAIL: Stabilizing Generative Adversarial Imitation Learning with Control Theory
Paper and Code
Feb 26, 2024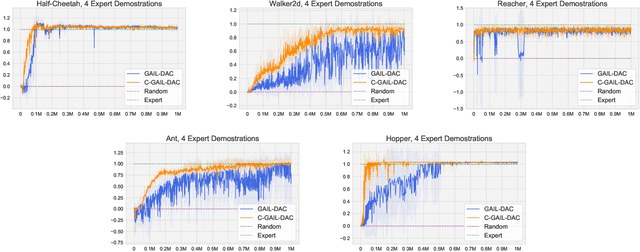

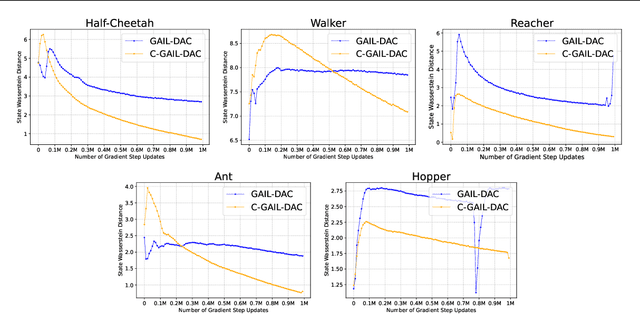
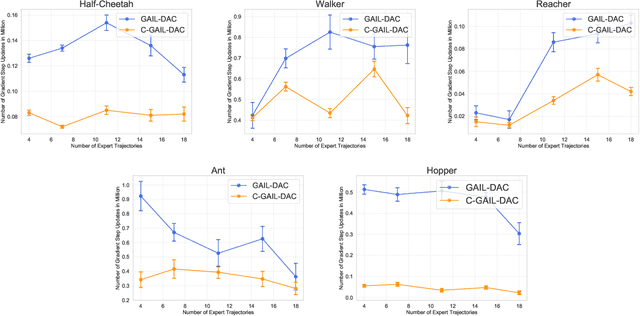
Generative Adversarial Imitation Learning (GAIL) trains a generative policy to mimic a demonstrator. It uses on-policy Reinforcement Learning (RL) to optimize a reward signal derived from a GAN-like discriminator. A major drawback of GAIL is its training instability - it inherits the complex training dynamics of GANs, and the distribution shift introduced by RL. This can cause oscillations during training, harming its sample efficiency and final policy performance. Recent work has shown that control theory can help with the convergence of a GAN's training. This paper extends this line of work, conducting a control-theoretic analysis of GAIL and deriving a novel controller that not only pushes GAIL to the desired equilibrium but also achieves asymptotic stability in a 'one-step' setting. Based on this, we propose a practical algorithm 'Controlled-GAIL' (C-GAIL). On MuJoCo tasks, our controlled variant is able to speed up the rate of convergence, reduce the range of oscillation and match the expert's distribution more closely both for vanilla GAIL and GAIL-DAC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge