Benchmarking Graph Neural Networks

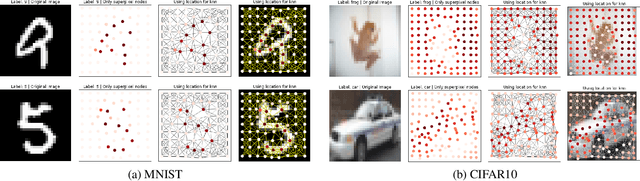
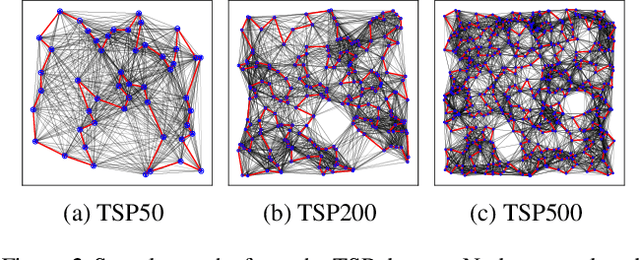
Graph neural networks (GNNs) have become the standard toolkit for analyzing and learning from data on graphs. They have been successfully applied to a myriad of domains including chemistry, physics, social sciences, knowledge graphs, recommendation, and neuroscience. As the field grows, it becomes critical to identify the architectures and key mechanisms which generalize across graphs sizes, enabling us to tackle larger, more complex datasets and domains. Unfortunately, it has been increasingly difficult to gauge the effectiveness of new GNNs and compare models in the absence of a standardized benchmark with consistent experimental settings and large datasets. In this paper, we propose a reproducible GNN benchmarking framework, with the facility for researchers to add new datasets and models conveniently. We apply this benchmarking framework to novel medium-scale graph datasets from mathematical modeling, computer vision, chemistry and combinatorial problems to establish key operations when designing effective GNNs. Precisely, graph convolutions, anisotropic diffusion, residual connections and normalization layers are universal building blocks for developing robust and scalable GNNs.