Bayesian Estimation of Differential Privacy
Paper and Code
Jun 15, 2022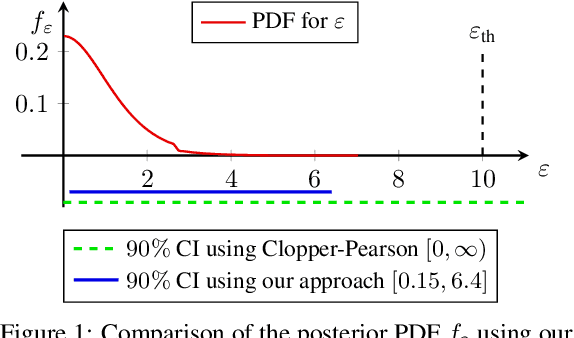

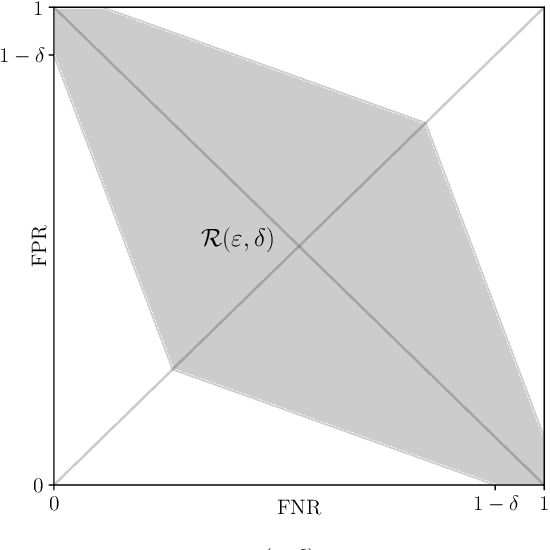
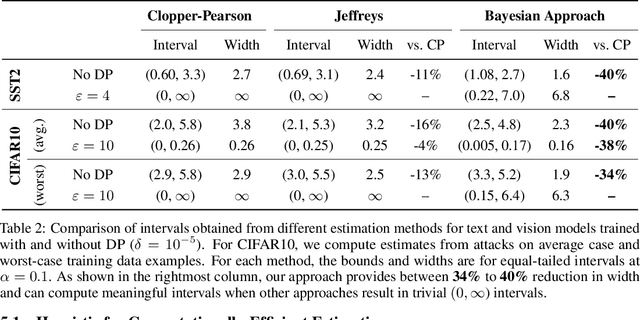
Algorithms such as Differentially Private SGD enable training machine learning models with formal privacy guarantees. However, there is a discrepancy between the protection that such algorithms guarantee in theory and the protection they afford in practice. An emerging strand of work empirically estimates the protection afforded by differentially private training as a confidence interval for the privacy budget $\varepsilon$ spent on training a model. Existing approaches derive confidence intervals for $\varepsilon$ from confidence intervals for the false positive and false negative rates of membership inference attacks. Unfortunately, obtaining narrow high-confidence intervals for $\epsilon$ using this method requires an impractically large sample size and training as many models as samples. We propose a novel Bayesian method that greatly reduces sample size, and adapt and validate a heuristic to draw more than one sample per trained model. Our Bayesian method exploits the hypothesis testing interpretation of differential privacy to obtain a posterior for $\varepsilon$ (not just a confidence interval) from the joint posterior of the false positive and false negative rates of membership inference attacks. For the same sample size and confidence, we derive confidence intervals for $\varepsilon$ around 40% narrower than prior work. The heuristic, which we adapt from label-only DP, can be used to further reduce the number of trained models needed to get enough samples by up to 2 orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge