BAMSProd: A Step towards Generalizing the Adaptive Optimization Methods to Deep Binary Model
Paper and Code
Sep 29, 2020
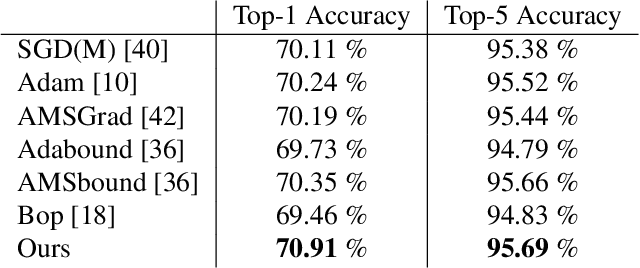

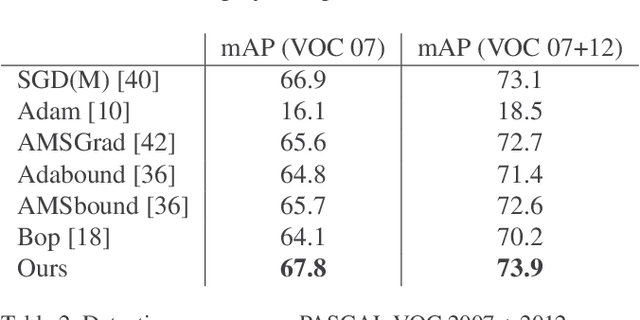
Recent methods have significantly reduced the performance degradation of Binary Neural Networks (BNNs), but guaranteeing the effective and efficient training of BNNs is an unsolved problem. The main reason is that the estimated gradients produced by the Straight-Through-Estimator (STE) mismatches with the gradients of the real derivatives. In this paper, we provide an explicit convex optimization example where training the BNNs with the traditionally adaptive optimization methods still faces the risk of non-convergence, and identify that constraining the range of gradients is critical for optimizing the deep binary model to avoid highly suboptimal solutions. For solving above issues, we propose a BAMSProd algorithm with a key observation that the convergence property of optimizing deep binary model is strongly related to the quantization errors. In brief, it employs an adaptive range constraint via an errors measurement for smoothing the gradients transition while follows the exponential moving strategy from AMSGrad to avoid errors accumulation during the optimization. The experiments verify the corollary of theoretical convergence analysis, and further demonstrate that our optimization method can speed up the convergence about 1:2x and boost the performance of BNNs to a significant level than the specific binary optimizer about 3:7%, even in a highly non-convex optimization problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge