Auto-PINN: Understanding and Optimizing Physics-Informed Neural Architecture
Paper and Code
May 27, 2022
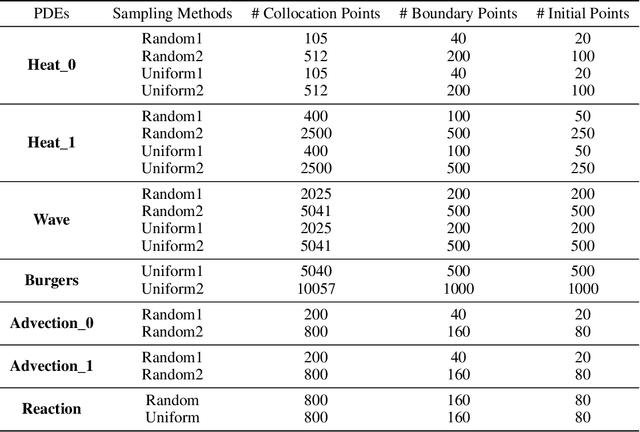
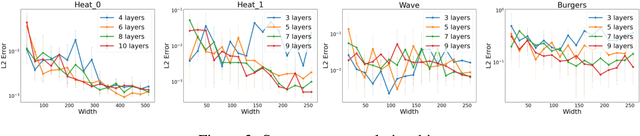
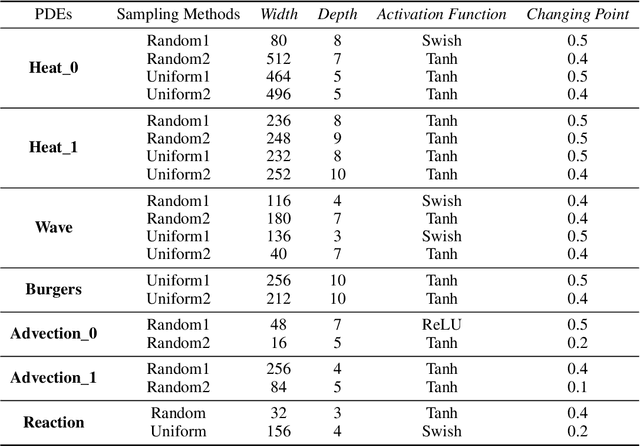
Physics-informed neural networks (PINNs) are revolutionizing science and engineering practice by bringing together the power of deep learning to bear on scientific computation. In forward modeling problems, PINNs are meshless partial differential equation (PDE) solvers that can handle irregular, high-dimensional physical domains. Naturally, the neural architecture hyperparameters have a large impact on the efficiency and accuracy of the PINN solver. However, this remains an open and challenging problem because of the large search space and the difficulty of identifying a proper search objective for PDEs. Here, we propose Auto-PINN, the first systematic, automated hyperparameter optimization approach for PINNs, which employs Neural Architecture Search (NAS) techniques to PINN design. Auto-PINN avoids manually or exhaustively searching the hyperparameter space associated with PINNs. A comprehensive set of pre-experiments using standard PDE benchmarks allows us to probe the structure-performance relationship in PINNs. We find that the different hyperparameters can be decoupled, and that the training loss function of PINNs is a good search objective. Comparison experiments with baseline methods demonstrate that Auto-PINN produces neural architectures with superior stability and accuracy over alternative baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge