AUC Maximization for Low-Resource Named Entity Recognition
Paper and Code
Dec 16, 2022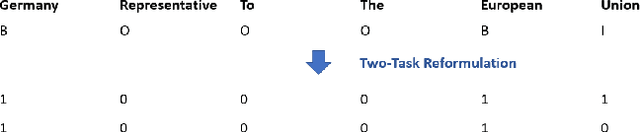

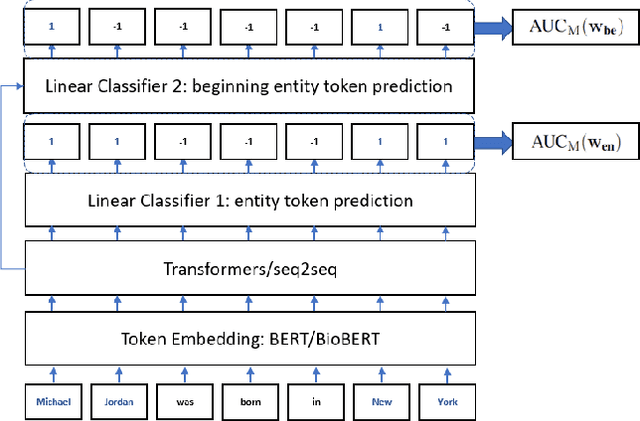
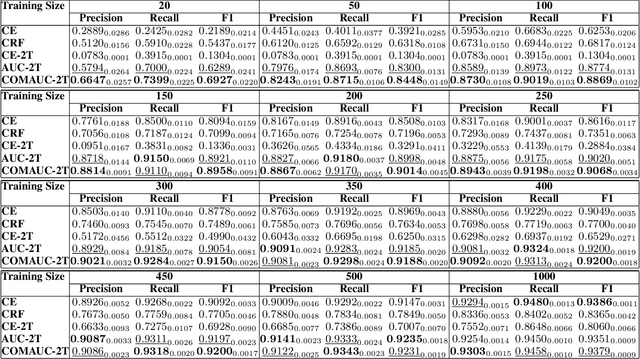
Current work in named entity recognition (NER) uses either cross entropy (CE) or conditional random fields (CRF) as the objective/loss functions to optimize the underlying NER model. Both of these traditional objective functions for the NER problem generally produce adequate performance when the data distribution is balanced and there are sufficient annotated training examples. But since NER is inherently an imbalanced tagging problem, the model performance under the low-resource settings could suffer using these standard objective functions. Based on recent advances in area under the ROC curve (AUC) maximization, we propose to optimize the NER model by maximizing the AUC score. We give evidence that by simply combining two binary-classifiers that maximize the AUC score, significant performance improvement over traditional loss functions is achieved under low-resource NER settings. We also conduct extensive experiments to demonstrate the advantages of our method under the low-resource and highly-imbalanced data distribution settings. To the best of our knowledge, this is the first work that brings AUC maximization to the NER setting. Furthermore, we show that our method is agnostic to different types of NER embeddings, models and domains. The code to replicate this work will be provided upon request.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge