ASAP: Architecture Search, Anneal and Prune
Paper and Code
Apr 08, 2019
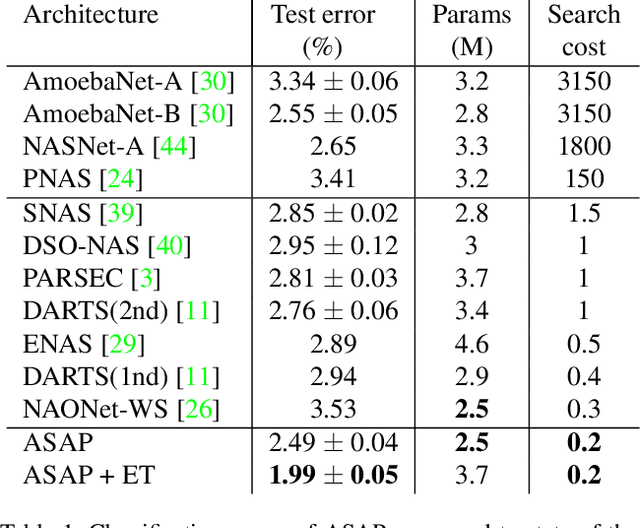
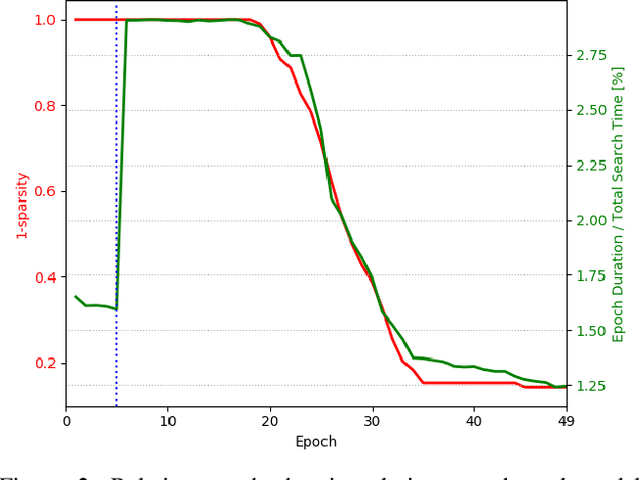
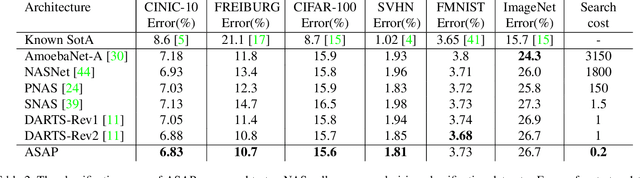
Automatic methods for Neural Architecture Search (NAS) have been shown to produce state-of-the-art network models, yet, their main drawback is the computational complexity of the search process. As some primal methods optimized over a discrete search space, thousands of days of GPU were required for convergence. A recent approach is based on constructing a differentiable search space that enables gradient-based optimization, thus reducing the search time to a few days. While successful, such methods still include some incontinuous steps, e.g., the pruning of many weak connections at once. In this paper, we propose a differentiable search space that allows the annealing of architecture weights, while gradually pruning inferior operations, thus the search converges to a single output network in a continuous manner. Experiments on several vision datasets demonstrate the effectiveness of our method with respect to the search cost, accuracy and the memory footprint of the achieved model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge