Approximating 1-Wasserstein Distance with Trees
Paper and Code
Jun 24, 2022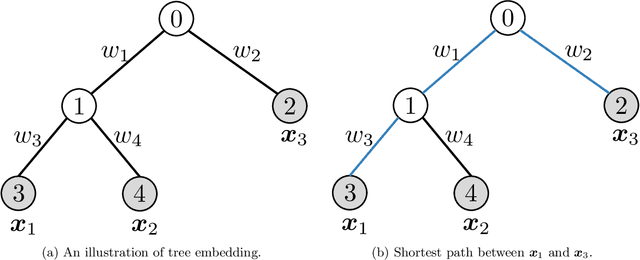
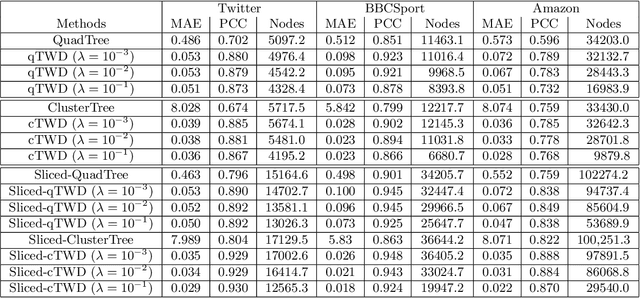
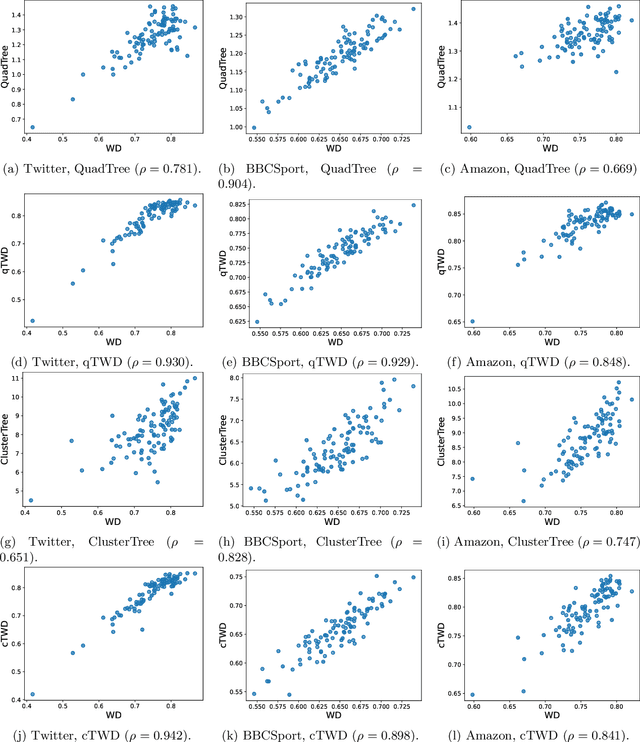
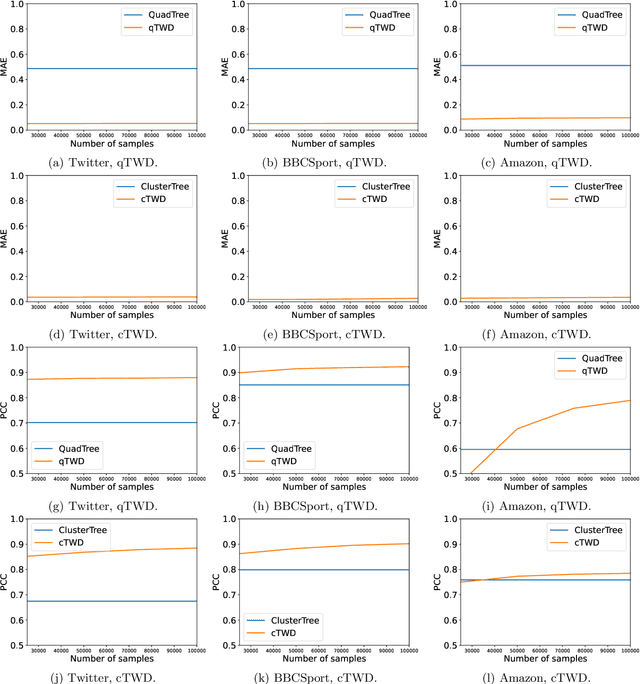
Wasserstein distance, which measures the discrepancy between distributions, shows efficacy in various types of natural language processing (NLP) and computer vision (CV) applications. One of the challenges in estimating Wasserstein distance is that it is computationally expensive and does not scale well for many distribution comparison tasks. In this paper, we aim to approximate the 1-Wasserstein distance by the tree-Wasserstein distance (TWD), where TWD is a 1-Wasserstein distance with tree-based embedding and can be computed in linear time with respect to the number of nodes on a tree. More specifically, we propose a simple yet efficient L1-regularized approach to learning the weights of the edges in a tree. To this end, we first show that the 1-Wasserstein approximation problem can be formulated as a distance approximation problem using the shortest path distance on a tree. We then show that the shortest path distance can be represented by a linear model and can be formulated as a Lasso-based regression problem. Owing to the convex formulation, we can obtain a globally optimal solution efficiently. Moreover, we propose a tree-sliced variant of these methods. Through experiments, we demonstrated that the weighted TWD can accurately approximate the original 1-Wasserstein distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge