Alternating Deep Low Rank Approach for Exponential Function Reconstruction and Its Biomedical Magnetic Resonance Applications

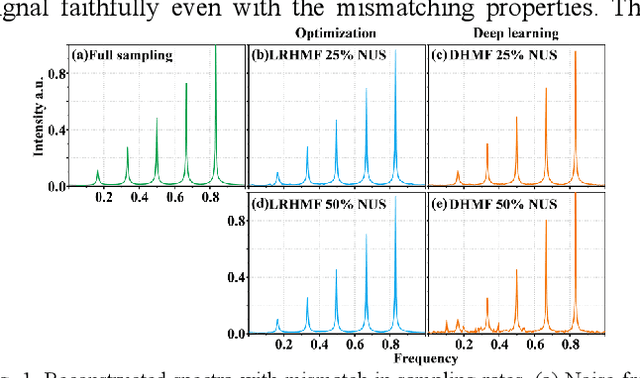
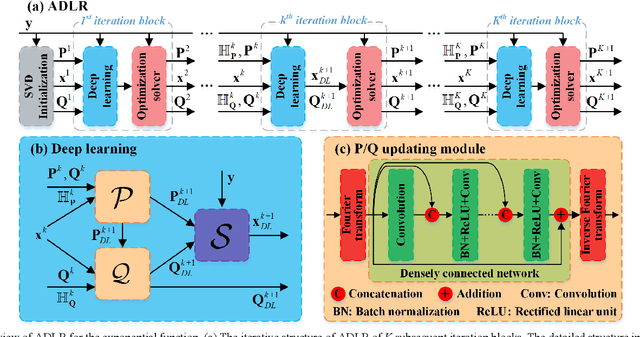
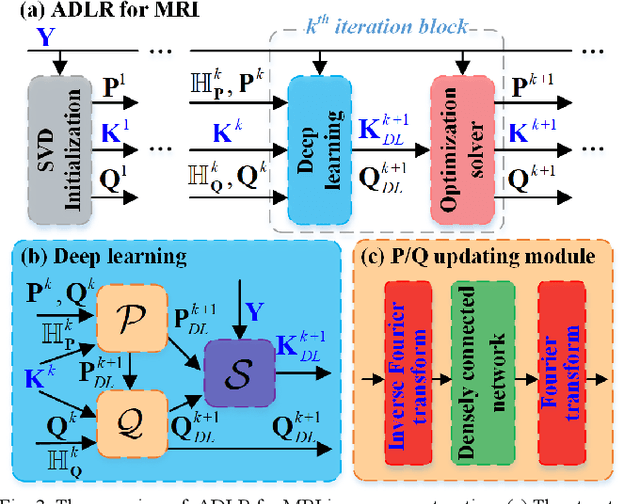
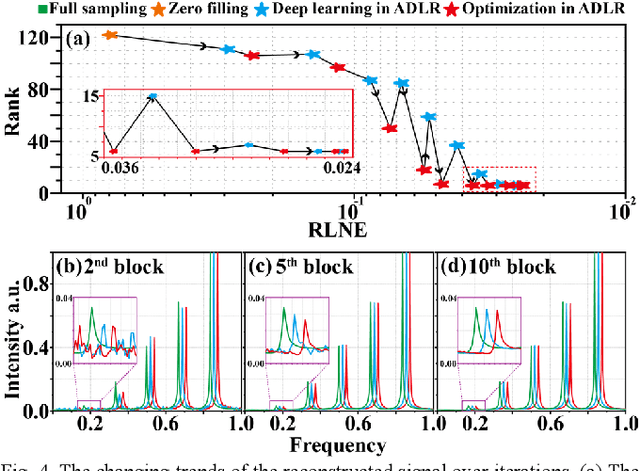
Exponential function is a fundamental signal form in general signal processing and biomedical applications, such as magnetic resonance spectroscopy and imaging. How to reduce the sampling time of these signals is an important problem. Sub-Nyquist sampling can accelerate signal acquisition but bring in artifacts. Recently, the low rankness of these exponentials has been applied to implicitly constrain the deep learning network through the unrolling of low rank Hankel factorization algorithm. However, only depending on the implicit low rank constraint cannot provide the robust reconstruction, such as sampling rate mismatches. In this work, by introducing the explicit low rank prior to constrain the deep learning, we propose an Alternating Deep Low Rank approach (ADLR) that utilizes deep learning and optimization solvers alternately. The former solver accelerates the reconstruction while the latter one corrects the reconstruction error from the mismatch. The experiments on both general exponential functions and realistic biomedical magnetic resonance data show that, compared with the state-of-the-art methods, ADLR can achieve much lower reconstruction error and effectively alleviates the decrease of reconstruction quality with sampling rate mismatches.