Adaptive Risk Minimization: A Meta-Learning Approach for Tackling Group Shift

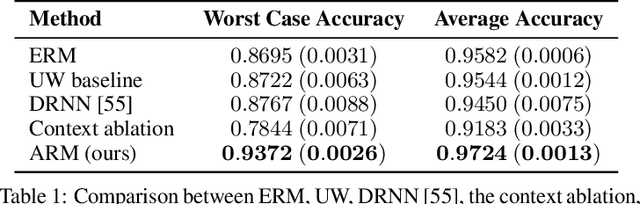
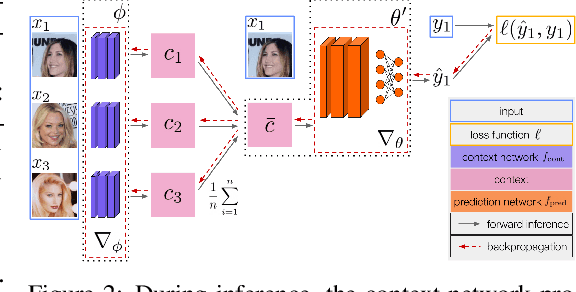
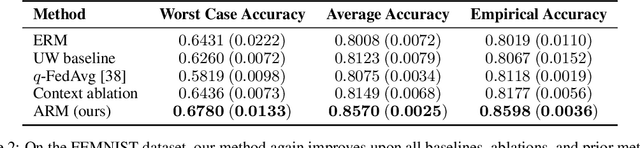
A fundamental assumption of most machine learning algorithms is that the training and test data are drawn from the same underlying distribution. However, this assumption is violated in almost all practical applications: machine learning systems are regularly tested on data that are structurally different from the training set, either due to temporal correlations, particular end users, or other factors. In this work, we consider the setting where test examples are not drawn from the training distribution. Prior work has approached this problem by attempting to be robust to all possible test time distributions, which may degrade average performance, or by "peeking" at the test examples during training, which is not always feasible. In contrast, we propose to learn models that are adaptable, such that they can adapt to distribution shift at test time using a batch of unlabeled test data points. We acquire such models by learning to adapt to training batches sampled according to different sub-distributions, which simulate structural distribution shifts that may occur at test time. We introduce the problem of adaptive risk minimization (ARM), a formalization of this setting that lends itself to meta-learning methods. Compared to a variety of methods under the paradigms of empirical risk minimization and robust optimization, our approach provides substantial empirical gains on image classification problems in the presence of distribution shift.