Adaptive Information Gathering via Imitation Learning
Paper and Code
May 22, 2017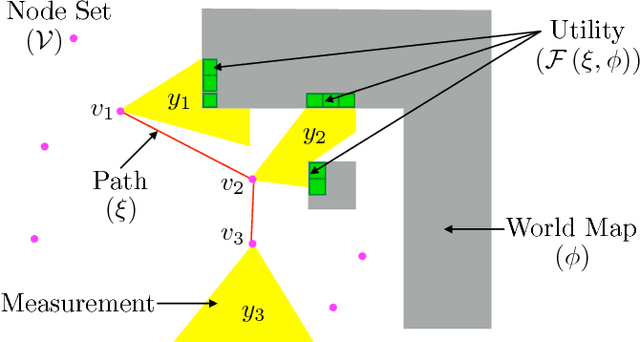

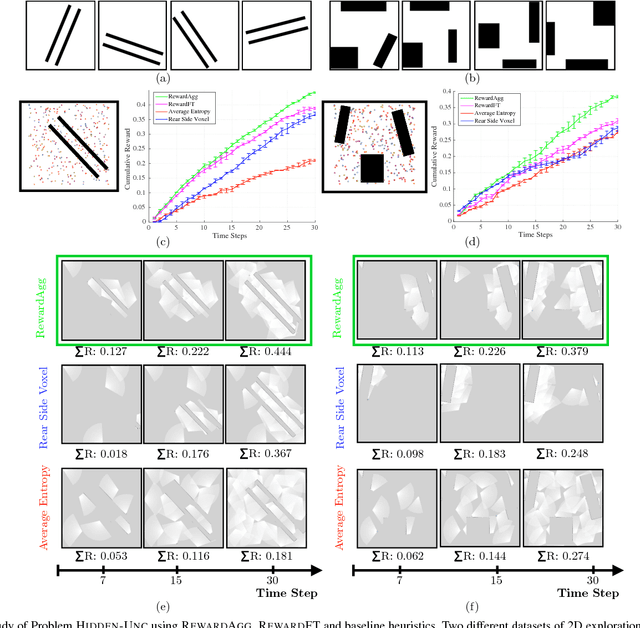

In the adaptive information gathering problem, a policy is required to select an informative sensing location using the history of measurements acquired thus far. While there is an extensive amount of prior work investigating effective practical approximations using variants of Shannon's entropy, the efficacy of such policies heavily depends on the geometric distribution of objects in the world. On the other hand, the principled approach of employing online POMDP solvers is rendered impractical by the need to explicitly sample online from a posterior distribution of world maps. We present a novel data-driven imitation learning framework to efficiently train information gathering policies. The policy imitates a clairvoyant oracle - an oracle that at train time has full knowledge about the world map and can compute maximally informative sensing locations. We analyze the learnt policy by showing that offline imitation of a clairvoyant oracle is implicitly equivalent to online oracle execution in conjunction with posterior sampling. This observation allows us to obtain powerful near-optimality guarantees for information gathering problems possessing an adaptive sub-modularity property. As demonstrated on a spectrum of 2D and 3D exploration problems, the trained policies enjoy the best of both worlds - they adapt to different world map distributions while being computationally inexpensive to evaluate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge