A Quasi-Newton Method Based Vertical Federated Learning Framework for Logistic Regression
Paper and Code
Dec 04, 2019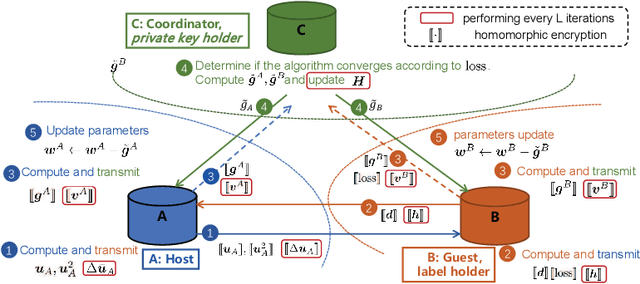
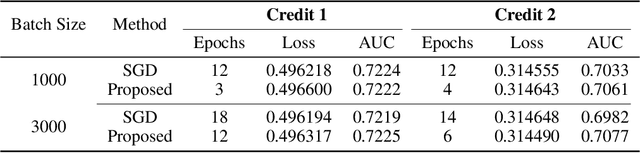
Data privacy and security becomes a major concern in building machine learning models from different data providers. Federated learning shows promise by leaving data at providers locally and exchanging encrypted information. This paper studies the vertical federated learning structure for logistic regression where the data sets at two parties have the same sample IDs but own disjoint subsets of features. Existing frameworks adopt the first-order stochastic gradient descent algorithm, which requires large number of communication rounds. To address the communication challenge, we propose a quasi-Newton method based vertical federated learning framework for logistic regression under the additively homomorphic encryption scheme. Our approach can considerably reduce the number of communication rounds with a little additional communication cost per round. Numerical results demonstrate the advantages of our approach over the first-order method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge