A New Adaptive Balanced Augmented Lagrangian Method with Application to ISAC Beamforming Design
Paper and Code
Oct 20, 2024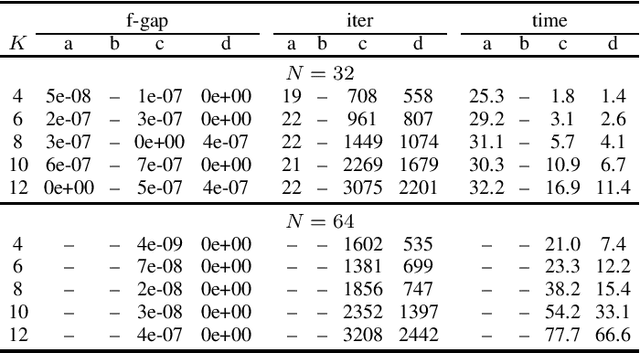
In this paper, we consider a class of convex programming problems with linear equality constraints, which finds broad applications in machine learning and signal processing. We propose a new adaptive balanced augmented Lagrangian (ABAL) method for solving these problems. The proposed ABAL method adaptively selects the stepsize parameter and enjoys a low per-iteration complexity, involving only the computation of a proximal mapping of the objective function and the solution of a linear equation. These features make the proposed method well-suited to large-scale problems. We then custom-apply the ABAL method to solve the ISAC beamforming design problem, which is formulated as a nonlinear semidefinite program in a previous work. This customized application requires careful exploitation of the problem's special structure such as the property that all of its signal-to-interference-and-noise-ratio (SINR) constraints hold with equality at the solution and an efficient computation of the proximal mapping of the objective function. Simulation results demonstrate the efficiency of the proposed ABAL method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge