A Comparison of Rule Extraction for Different Recurrent Neural Network Models and Grammatical Complexity

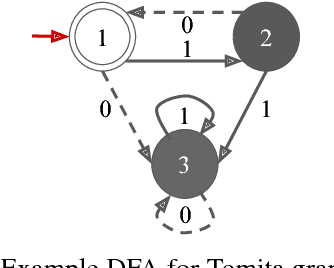
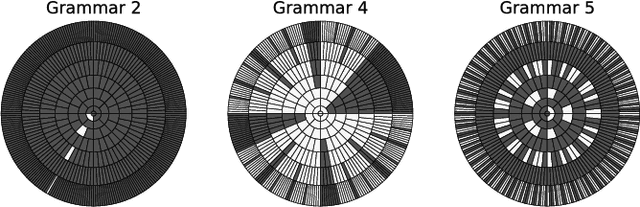
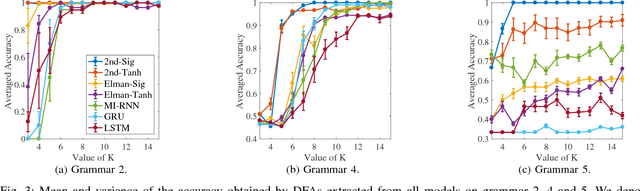
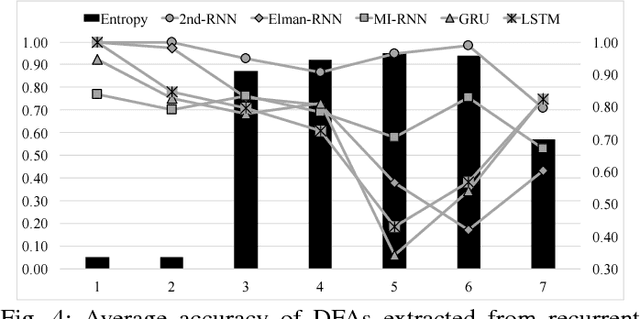
It has been shown that rules can be extracted from highly non-linear, recursive models such as recurrent neural networks (RNNs). The RNN models mostly investigated include both Elman networks and second-order recurrent networks. Recently, new types of RNNs have demonstrated superior power in handling many machine learning tasks, especially when structural data is involved such as language modeling. Here, we empirically evaluate different recurrent models on the task of learning deterministic finite automata (DFA), the seven Tomita grammars. We are interested in the capability of recurrent models with different architectures in learning and expressing regular grammars, which can be the building blocks for many applications dealing with structural data. Our experiments show that a second-order RNN provides the best and stablest performance of extracting DFA over all Tomita grammars and that other RNN models are greatly influenced by different Tomita grammars. To better understand these results, we provide a theoretical analysis of the "complexity" of different grammars, by introducing the entropy and the averaged edit distance of regular grammars defined in this paper. Through our analysis, we categorize all Tomita grammars into different classes, which explains the inconsistency in the performance of extraction observed across all RNN models.