A Benchmark Study of Deep-RL Methods for Maximum Coverage Problems over Graphs
Paper and Code
Jun 20, 2024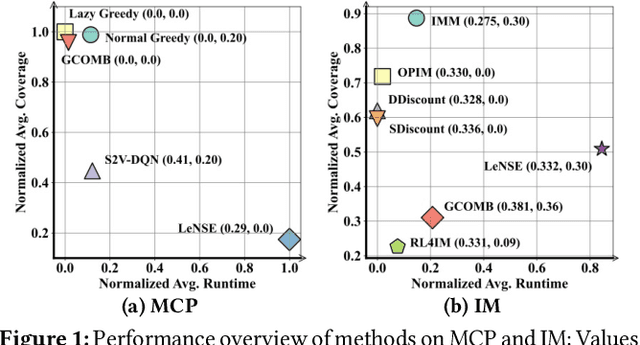
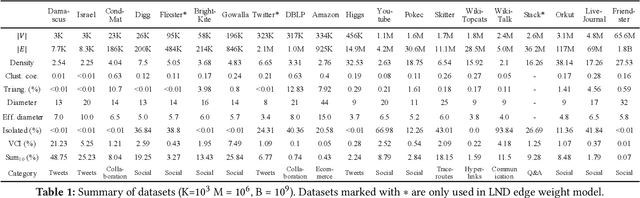
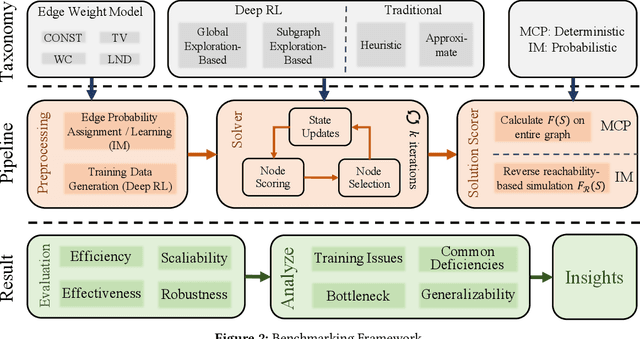
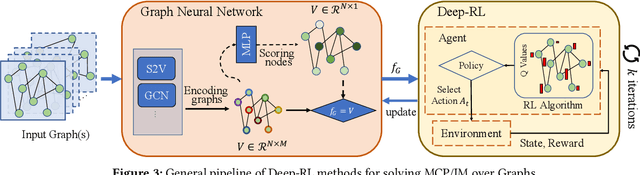
Recent years have witnessed a growing trend toward employing deep reinforcement learning (Deep-RL) to derive heuristics for combinatorial optimization (CO) problems on graphs. Maximum Coverage Problem (MCP) and its probabilistic variant on social networks, Influence Maximization (IM), have been particularly prominent in this line of research. In this paper, we present a comprehensive benchmark study that thoroughly investigates the effectiveness and efficiency of five recent Deep-RL methods for MCP and IM. These methods were published in top data science venues, namely S2V-DQN, Geometric-QN, GCOMB, RL4IM, and LeNSE. Our findings reveal that, across various scenarios, the Lazy Greedy algorithm consistently outperforms all Deep-RL methods for MCP. In the case of IM, theoretically sound algorithms like IMM and OPIM demonstrate superior performance compared to Deep-RL methods in most scenarios. Notably, we observe an abnormal phenomenon in IM problem where Deep-RL methods slightly outperform IMM and OPIM when the influence spread nearly does not increase as the budget increases. Furthermore, our experimental results highlight common issues when applying Deep-RL methods to MCP and IM in practical settings. Finally, we discuss potential avenues for improving Deep-RL methods. Our benchmark study sheds light on potential challenges in current deep reinforcement learning research for solving combinatorial optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge