2D-Shapley: A Framework for Fragmented Data Valuation
Paper and Code
Jun 18, 2023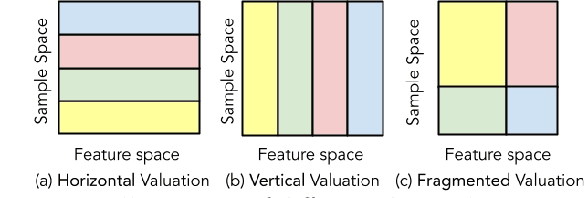

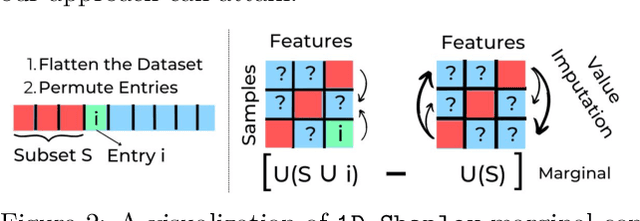
Data valuation -- quantifying the contribution of individual data sources to certain predictive behaviors of a model -- is of great importance to enhancing the transparency of machine learning and designing incentive systems for data sharing. Existing work has focused on evaluating data sources with the shared feature or sample space. How to valuate fragmented data sources of which each only contains partial features and samples remains an open question. We start by presenting a method to calculate the counterfactual of removing a fragment from the aggregated data matrix. Based on the counterfactual calculation, we further propose 2D-Shapley, a theoretical framework for fragmented data valuation that uniquely satisfies some appealing axioms in the fragmented data context. 2D-Shapley empowers a range of new use cases, such as selecting useful data fragments, providing interpretation for sample-wise data values, and fine-grained data issue diagnosis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge