10,000+ Times Accelerated Robust Subset Selection (ARSS)

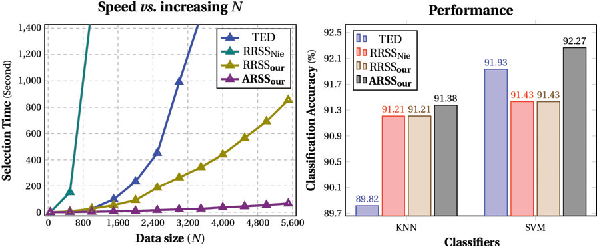
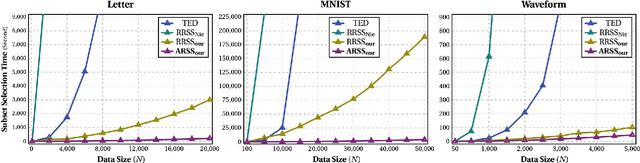
Subset selection from massive data with noised information is increasingly popular for various applications. This problem is still highly challenging as current methods are generally slow in speed and sensitive to outliers. To address the above two issues, we propose an accelerated robust subset selection (ARSS) method. Specifically in the subset selection area, this is the first attempt to employ the $\ell_{p}(0<p\leq1)$-norm based measure for the representation loss, preventing large errors from dominating our objective. As a result, the robustness against outlier elements is greatly enhanced. Actually, data size is generally much larger than feature length, i.e. $N\gg L$. Based on this observation, we propose a speedup solver (via ALM and equivalent derivations) to highly reduce the computational cost, theoretically from $O(N^{4})$ to $O(N{}^{2}L)$. Extensive experiments on ten benchmark datasets verify that our method not only outperforms state of the art methods, but also runs 10,000+ times faster than the most related method.