Two-Channel Extended Kalman Filtering with Intermittent Measurements

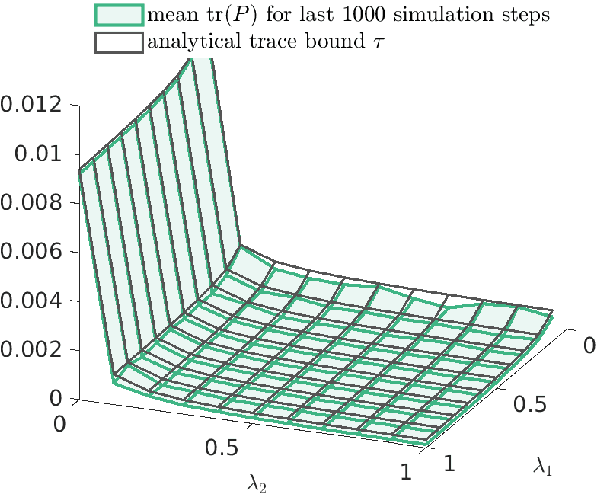
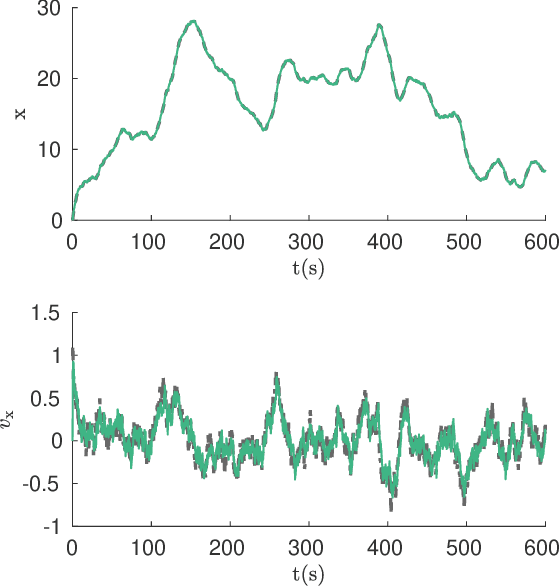
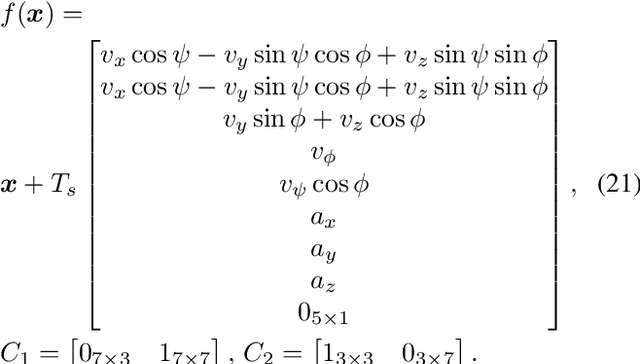
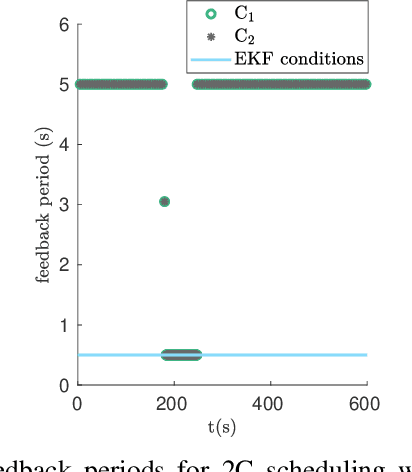
We consider two nonlinear state estimation problems in a setting where an extended Kalman filter receives measurements from two sets of sensors via two channels (2C). In the stochastic-2C problem, the channels drop measurements stochastically, whereas in 2C scheduling, the estimator chooses when to read each channel. In the first problem, we generalize linear-case 2C analysis to obtain -- for a given pair of channel arrival rates -- boundedness conditions for the trace of the error covariance, as well as a worst-case upper bound. For scheduling, an optimization problem is solved to find arrival rates that balance low channel usage with low trace bounds, and channels are read deterministically with the expected periods corresponding to these arrival rates. We validate both solutions in simulations for linear and nonlinear dynamics; as well as in a real experiment with an underwater robot whose position is being intermittently found in a UAV camera image.

3D exploration-based search for multiple targets using a UAV

Consider an unmanned aerial vehicle (UAV) that searches for an unknown number of targets at unknown positions in 3D space. A particle filter uses imperfect measurements about the targets to update an intensity function that represents the expected number of targets. We propose a receding-horizon planner that selects the next UAV position by maximizing a joint, exploration and target-refinement objective. Confidently localized targets are saved and removed from consideration. A nonlinear controller with an obstacle-avoidance component is used to reach the desired waypoints. We demonstrate the performance of our approach through a series of simulations, as well as in real-robot experiments with a Parrot Mambo drone that searches for targets from a constant altitude. The proposed planner works better than a lawnmower and a target-refinement-only method.