Two-Channel Extended Kalman Filtering with Intermittent Measurements
Paper and Code
Dec 18, 2023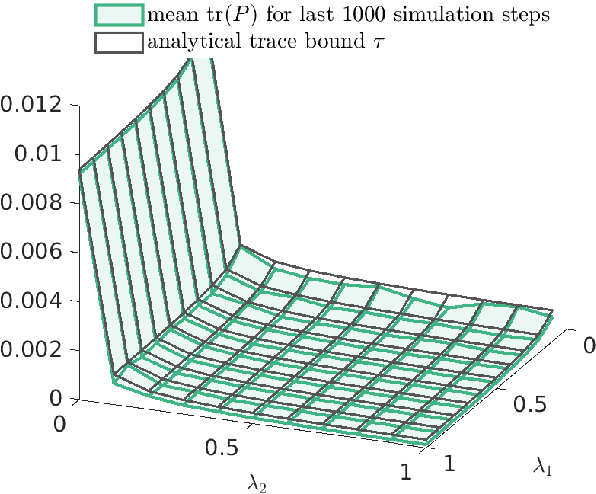
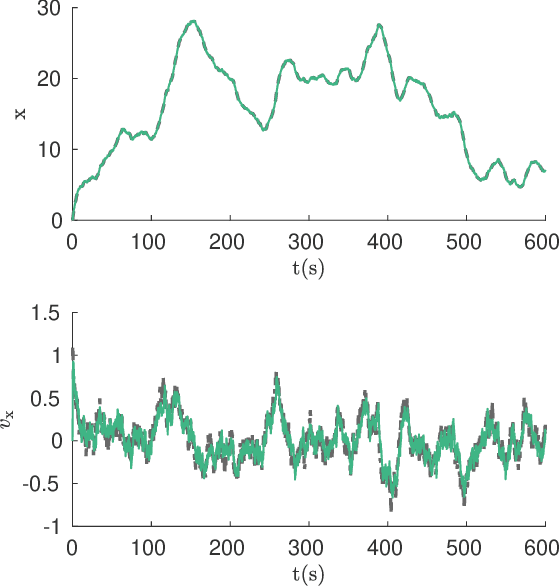
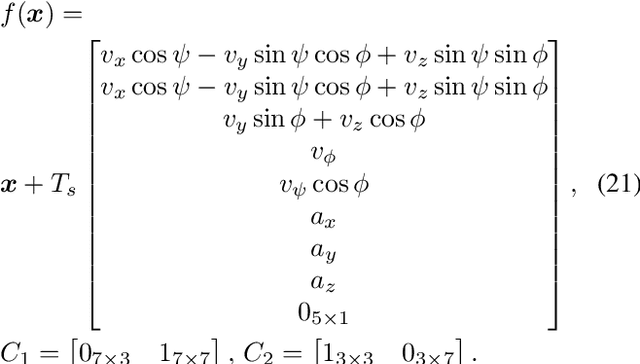
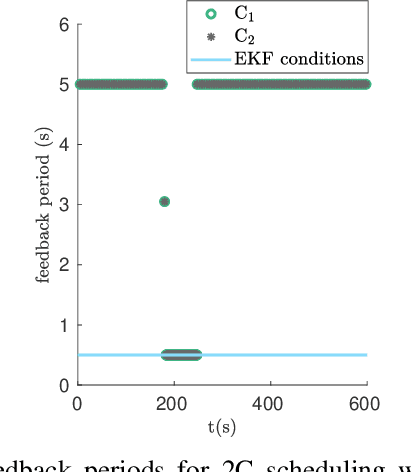
We consider two nonlinear state estimation problems in a setting where an extended Kalman filter receives measurements from two sets of sensors via two channels (2C). In the stochastic-2C problem, the channels drop measurements stochastically, whereas in 2C scheduling, the estimator chooses when to read each channel. In the first problem, we generalize linear-case 2C analysis to obtain -- for a given pair of channel arrival rates -- boundedness conditions for the trace of the error covariance, as well as a worst-case upper bound. For scheduling, an optimization problem is solved to find arrival rates that balance low channel usage with low trace bounds, and channels are read deterministically with the expected periods corresponding to these arrival rates. We validate both solutions in simulations for linear and nonlinear dynamics; as well as in a real experiment with an underwater robot whose position is being intermittently found in a UAV camera image.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge